Simulação do problema de Monty Hall em R

Simulação do problema de Monty Hall em R

O problema de Monty Hall surgiu e foi nomeado pelo nome do apresentador de um programa de televisão dos anos 70, nos EUA, similar com o que vemos no Sílvio Santos aqui no Brasil. Pelo nome pode não lembrar, mas deve lembrar pela cena do excelente filme “Quebrando a Banca”. (caso não tenha visto, recomendamos bastante!)

Você tem 3 portas na sua frente: uma com um carro e outras duas com bodes, apenas não sabe quais são. Logo após você escolher uma porta, Monty, que sabe qual tem o carro, abre uma com um bode por trás, e pergunta: “Você gostaria de manter ou trocar a porta escolhida?”

Algo parece estranho… Se você troca a porta, existe 50% de chance de ter um bode ou de ter um carro, torna-se aleatório, certo? Na verdade, não. Como você escolheu uma porta ao acaso, há maior chance de ter inicialmente escolhido com um bode atrás (2 possibilidades em 3, ou 2/3 = 67%) e, como Monty Hall mostra a porta que tem um bode, você tem mais chance de trocar para uma que realmente tenha o prêmio.

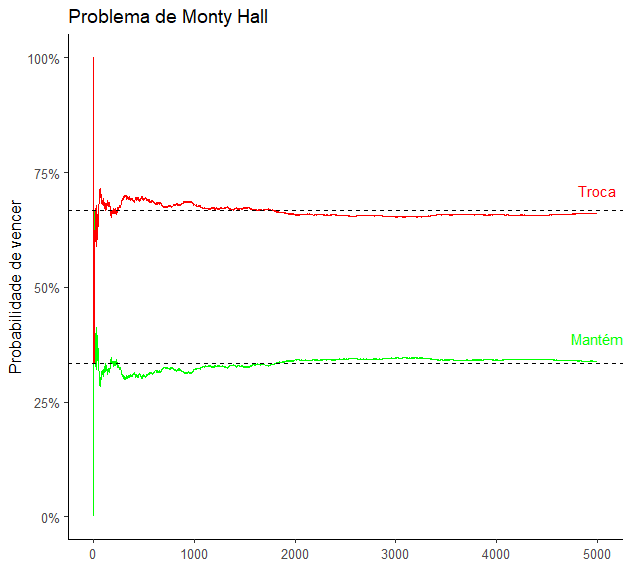
Assim, a estratégia de manter a porta te dá 1/3 de chance de acertar, enquanto trocando suas chances dobram, indo para 2/3!

Como podemos achar essas probabilidades simulando vários jogos? É isso que vamos explorar a seguir:

Iniciando as variáveis do jogo

library(tidyverse) # Pacote para limpeza e visualização de dados
library(grid)      # Nos auxiliará para fazer anotações nos gráficos
library(ggpubr)    # Temas já personalizados

set.seed(1970) # Homenagem à década que o programa foi ao ar
               # Ter o mesmo valor permite que tenha os mesmos resultados do código abaixo

n <- 5000 # Número de programas que simularemos

resultados <- matrix(data = NA, # Matriz vazia; usaremos para preenchermos os resultados 
                     ncol = 3,  # Três colunas: número do jogo e se acerta mantendo ou trocando a porta
                     nrow = n)  # Quantidade de jogos, um em cada linha
                    
resultados[,1] <- 1:n # Enumerando os jogos, de 1 até n (5000 nesse caso)                    

Modelando o desenrolar do jogo

for(i in c(1:n)) {
  
  portas = rep(NA, 3) # Novas portas
  
  portas[sample(1:3, 1)] = 1 # Apenas uma delas contém o prêmio, designada ao acaso
  
  portas[is.na(portas) == TRUE] = 0 # Quais não contém prêmio são aquelas que tem bodes
  
  jogador = sample(1:3, 1) # Jogador escolhe uma das 3 portas ao acaso
  
  jogo = matrix(data = c( portas, c(1:3) ), nrow = 2, byrow = TRUE) # Apenas juntando as informações do jogo até aqui
  
  jogo_apresentador = jogo[1,] # O apresentador, porém, conhece o jogo e qual a porta vencedora
  
  jogo_apresentador[jogador] = "NÃO USAR"  # Obviamente, o apresentador não abrirá a porta que o jogador tenha escolhido
  
  reveal = which(jogo_apresentador %in% "0") # Sabendo que existe outra porta com o bode, o apresentador a escolhe
  
  if(length(reveal) == 2) {
    
    reveal = sample(reveal, 1)
    
  }

Organizando os resultados para visualizarmos graficamente

df_resultados <- as.data.frame(resultados) # Transformando em data.frame

names(df_resultados) <- c("Iteração", "Mantém", "Troca") # Modificando os nomes

df_resultados$Mantém <- cummean(df_resultados$Mantém) # Observando a média de acertos ao longo dos jogos 
df_resultados$Troca <- cummean(df_resultados$Troca)

df_resultados_gather <- gather(df_resultados,       # Organizando os dados num formato longo
                               key = "Estratégia",  # Colocar "Mantém" e "Troca" numa coluna apenas
                               value = "Acertos",
                               -Iteração)

Visualização gráfica (utilizando ggplot2)

ggplot(data = df_resultados_gather, mapping = aes(x = Iteração,           # Número do jogo em X
                                                  y = Acertos,            # Valor da probabilidade de acerto em Y
                                                  colour = Estratégia)) + # Colorindo as curvas por tipo de estratégia
geom_line() + # Fazendo o gráfico das curvas
geom_hline(yintercept = 1/3,
           lty = 2,
           lwd = 0.5) + # Colocando no gráfico a probabilidade verdadeira de ganhar não trocando
geom_hline(yintercept = 2/3,
           lty = 2,
           lwd = 0.5) + # Colocando no gráfico a probabilidade verdadeira de ganhar trocando
geom_text(data = subset(df_resultados_gather, Iteração == n),
        aes(label = Estratégia, 
            colour = Estratégia, 
            x = n, 
            y = Acertos + 0.05)) + # Marcando no gráfico os nomes das curvas
ggpubr::theme_classic2() + # Tema já pronto para uso
scale_y_continuous(labels = scales::percent_format()) + # Colocando o eixo Y em percentual
labs(x = NULL,
     y = "Probabilidade de vencer",
     title = "Problema de Monty Hall") + # Trocando os títulos dos eixos
theme(legend.position = "none") + # Retirando a legenda
scale_color_manual(values = c("green", "red")) # Mudando manualmente as cores das curvas