Motivação para análise empírica

Uma característica proeminente dos cursos de macroeconomia em nível de graduação inicial é o conceito de produto potencial. O produto potencial é de interesse para os macroeconomistas ao analisar a questão dos hiatos do produto e das políticas de estabilização macroeconômica dos governos, seja em uma expansão ou recessão econômica. Se uma economia tem um hiato do produto positivo, então dizemos que a economia está operando acima do seu nível potencial, e as pressões inflacionárias aumentarão à medida que os fatores de produção exigirem preços cada vez mais altos para serem usados no processo produtivo. O mesmo racioncío pode ser estendido para o hiato do produto negativo.

Uma forma simples e elegante de estimar a série do hiato do produto de uma economia é estimar o desvio do logaritmo do produto potencial. Essa medida construída como o desvio do logaritmo corresponde, de forma aproximada, a um desvio percentual do produto potencial. Como forma de capturar a tendência de longo prazo da série do produto interno bruto de uma economia, será implementado o filtro Hodrick-Prescott (HP), método extensivamente utilizado em macroeconomia para descrever comportamento de variáveis macroeconomicas e seus co-movimentos.

O Filtro HP decompõe as observações na soma de um componente de tendência, $x_{t}^{t}$, e um componente cíclico, $x_{t}^{c}$, isto é:

$$ \begin{equation} x_{t}=x_{t}^{t}+x_{t}^{c} \end{equation} $$

de tal sorte que a série $x_{t}^{t}$ é escolhida pela minimização de: $$ \begin{equation} \min _{x_{t}^{t}} \sum_{t=1}^{T}\left(x_{t}-x_{t}^{t}\right)^{2}+\lambda \sum_{t=2}^{T-1}\left[\left(x_{t+1}^{t}-x_{t}^{t}\right)-\left(x_{t}^{t}-x_{t-1}^{t}\right)\right]^{2} \end{equation} $$ onde o primeiro termo corresponde aos desvios ao quadrado de $x_{t}$ em relação a $x_{t}^{t}$, e o segundo termo é uma penalização que restringe a segunda diferença de $x_{t}^{t}$, e o parâmetro $\lambda$ controla a suavidade da série $x_{t}^{t}$.

Antes de começar a análise, é necessário que os pacotes abaixo sejam carregados. O pacote BETS é uma ótima alternativa para importar os dados direto do Sistema Gerenciador de Séries Temporais - (SGS), do Banco Central do Brasil (BCB). Tidyverse é uma coleção The tidyverse de pacotes do R projetados para data science. O pacote ggplot2 permite a criação amigável de gráficos para a séries econômicas. Por último, o pacote mFilter será utilizado para implementação do filtro HP.

library(BETS)
library(tidyverse)
library(ggplot2)
library(mFilter)

Baixando as séries de Produto Interno Bruto

O proximo chunk mostra como obter a série do Produto Interno Bruto (PIB) trimestral, com e sem ajuste sazonal, a preços de mercado direto do SGS. Em seguida, são obtidas as séries do PIB trimestral em logaritmo e as taxas de crescimento trimestral, respectivamente.

gdp <- BETSget(22099, data.frame = TRUE) # Série do PIB trimestral, sem ajuste sazonal

gdp_s <- BETSget(22109, data.frame = TRUE) # Série do PIB trimestral, com ajuste sazonal

gdp <- gdp %>%
  as_tibble() %>%
  filter(date >= "1996-01-01") %>%
  mutate(lgdp = log(value),
         dlgdp = 100*(lgdp - lag(lgdp, 4))) %>%
  drop_na()

gdp_s <- gdp_s %>%
  as_tibble() %>%
  filter(date >= "1996-01-01") %>%
  mutate(lgdp_s = log(value),
         dlgdp_s = 100*(lgdp_s - lag(lgdp_s, 1))) %>%
  drop_na()

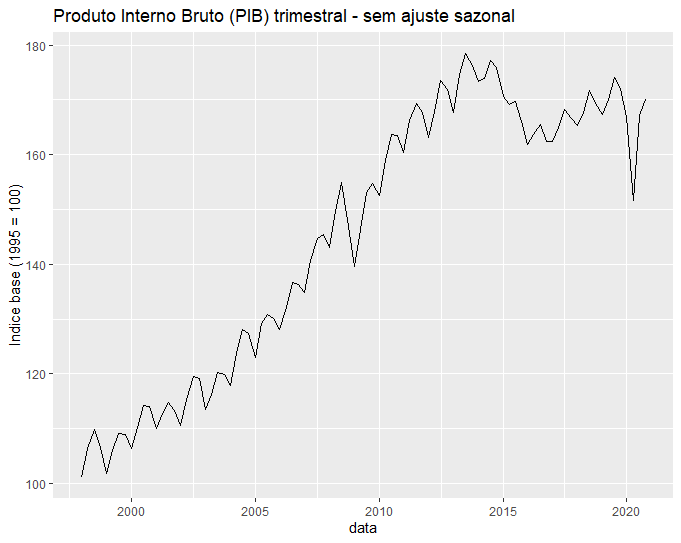
Para visualização das séries do PIB (com e sem ajuste sazonal) em nível, considere os seguintes gráficos de linhas:

gdp %>% 
  ggplot(aes(x = date, y = value)) +
  geom_line() +
  labs(title = "Produto Interno Bruto (PIB) trimestral - sem ajuste sazonal",
       y = "Indice base (1995 = 100)" , x = 'data') + 
  theme_gray()

gdp_s %>% 
  ggplot(aes(x = date, y = value)) +
  geom_line() +
  labs(title = "Produto Interno Bruto (PIB) trimestral - com ajuste sazonal",
       y = "Indice base (1995 = 100)" , x = 'data') + 
  theme_gray()

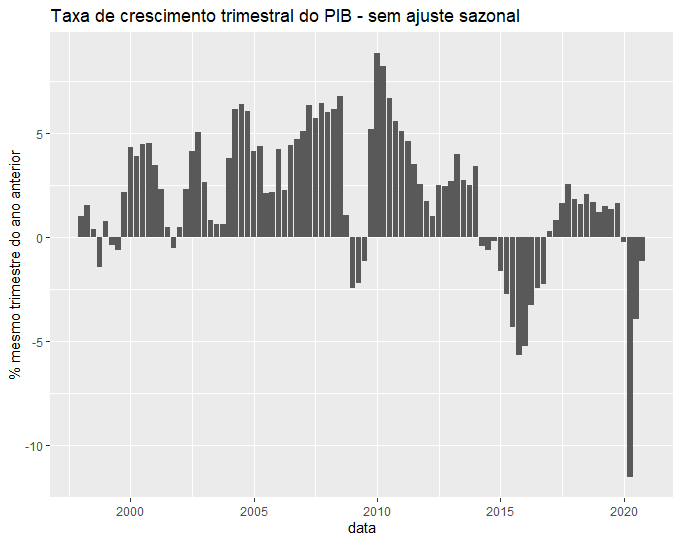
Para visualização das taxas de crescimento trimestral do PIB, considere os seguintes gráficos de barras:

gdp %>% 
  ggplot(aes(x = date, y = dlgdp)) +
  geom_col() +
  labs(title = "Taxa de crescimento trimestral do PIB - sem ajuste sazonal",
       y = "% mesmo trimestre do ano anterior", x = 'data') + 
  theme_grey()

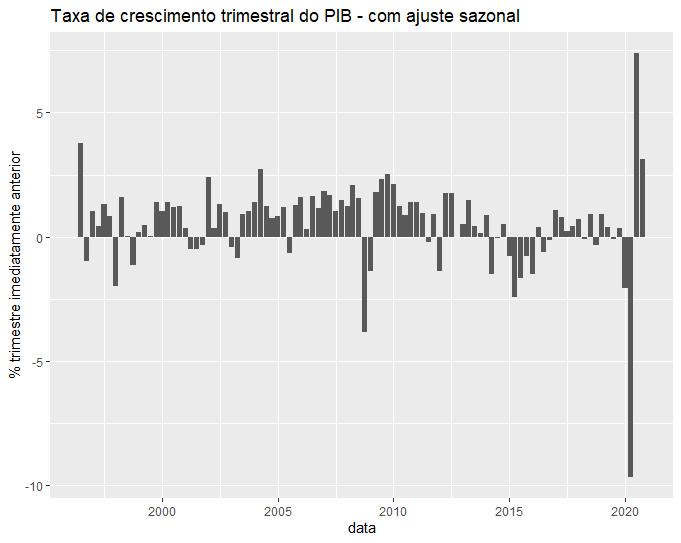
gdp_s %>% 
  ggplot(aes(x = date, y = dlgdp_s)) +
  geom_col() +
  labs(title = "Taxa de crescimento trimestral do PIB - com ajuste sazonal",
       y = "% trimestre imediatamente anterior", x = 'data') + 
  theme_grey()

Filtro Hodrick-Prescott

Usualmente, o parâmetro de suavização $\lambda$ do filtro HP, de Hodrick e Prescott, pode ser definido de acordo com a frequência da série temporal: como a análise considera uma série com frequência trimestral, $\lambda = 1.600$. Outros valores são considerados para séries de outras frequências, a saber, anual e mensal, com valores $\lambda = 100$ e $\lambda = 14.400$, respectivamente. Por hora, seguiremos apenas com o PIB trimestral do Brasil, com ajuste sazonal. Considere a estimação do filtro HP:

hp_filter <- hpfilter(gdp_s$lgdp_s, freq = 1600)

gdp_s_filter <- gdp_s %>%
  mutate(output_gap = hp_filter$cycle,
         trend = hp_filter$trend)

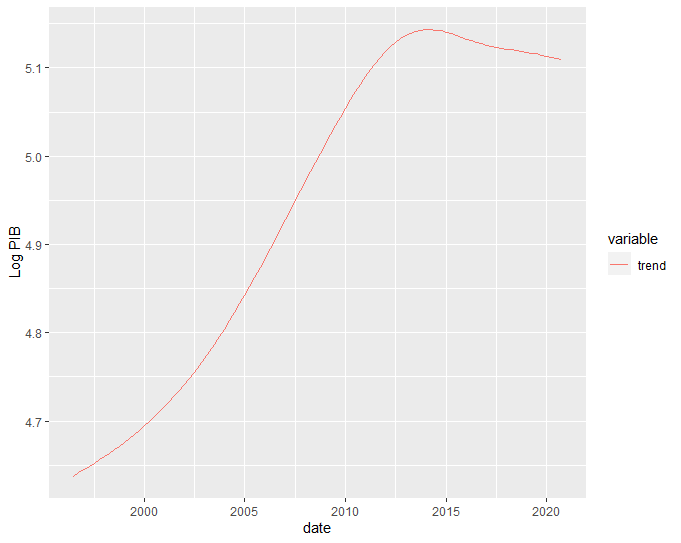
Para visualização do componente de tendência de longo prazo da série do logaritmo do PIB trimestral, considere o seguinte gráfico de linhas:

gdp_s_filter %>% 
  pivot_longer(-date, names_to = "variable", values_to = "value") %>% 
  drop_na() %>% 
  filter(variable %in% c("trend")) %>% 
  ggplot(aes(date, value, color = variable)) +
  labs(y = "Log PIB") +
  geom_line() +
  theme_grey()

Conforme discutido no ínício da análise, o componente de tendência de longo prazo da série do PIB trimestral pode ser tomado como o PIB potencial brasileiro. Para contrastar, considere a comparação da série com o PIB realizado

gdp_s_filter %>% 
  pivot_longer(-date, names_to = "variable", values_to = "value") %>% 
  drop_na() %>% 
  filter(variable %in% c("trend","lgdp_s")) %>% 
  ggplot(aes(date, value, color = variable)) +
  labs(y = "Log PIB") +
  geom_line() +
  theme_grey()

De acordo com a teoria macroeconômica, o hiato do produto é definido pela diferença entre o PIB observado e PIB potencial. Coincidentemente, o componente cíclico estimado pelo fltro determina exatamente essa diferença. Logo, para visualização do componente cíclico da série do logaritmo do PIB trimestral, considere o seguinte gráfico de linhas:

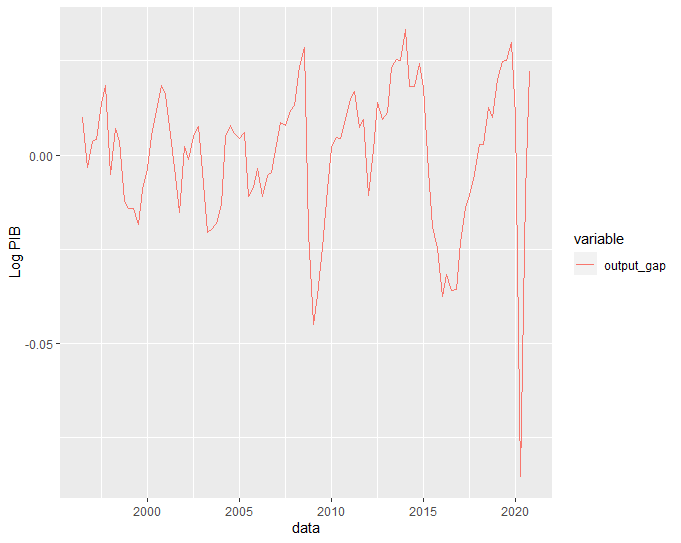
gdp_s_filter %>% 
  pivot_longer(-date, names_to = "variable", values_to = "value") %>% 
  drop_na() %>% 
  filter(variable %in% c("output_gap")) %>% 
  ggplot(aes(date, value, color = variable)) +
  labs(y = "Log PIB", x = 'data') +
  geom_line() +
  theme_grey()