Fronteira Eficiente estimada por Python

Nesse post o Victor Gomes do Trading com Dados estima a fronteira eficiente de ativos da bolsa brasileira. Importando bibliotecas.

import pandas as pd
import numpy as np
from pandas_datareader import data as wb
import matplotlib.pyplot as plt
import seaborn as sns

Selecionando ativos da carteira.

ativos = ['ABEV3.SA', 'EQTL3.SA', 'LREN3.SA', 'CIEL3.SA', 'RADL3.SA', 'RENT3.SA', 'MDIA3.SA', 'WEGE3.SA', 'EZTC3.SA', 'FLRY3.SA']

Criando um dataframe que vai conter as cotações diárias dessas ações.

df = pd.DataFrame()

for t in ativos:
  df[t] = wb.DataReader(t, data_source = 'yahoo', start = '2014-01-01', end = '2021-05-03')['Adj Close']

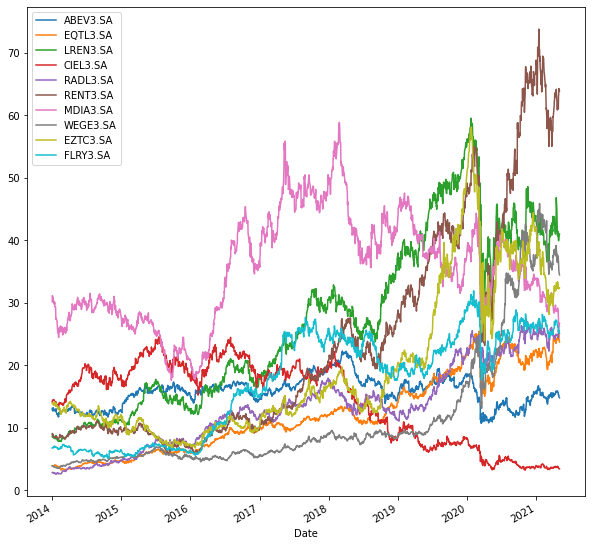
Visualizando os preços.

df.plot(figsize = (10,10))

Visualizando o dataframe.

df.head()

Calculando retorno diário dos papéis e tratando os dados.

retorno_diario = df.pct_change()

retorno_diario.head()
retorno_diario = retorno_diario.iloc[1:]
retorno_diario.head()

Calculando o retorno anual.

retorno_anual = retorno_diario.mean()*250

Matriz de covariância.

cov_diario = retorno_diario.cov()

cov_diario

cov_anual = cov_diario*250

Aqui vamos criar 200 mil portfólios fictícios com esses papéis.

port_returns = []

port_volatility = []

stock_weights = []

Vamos passar os parâmetros de simulação.

num_assets = len(ativos)

num_portfolios = 200000

Vamos usar a função random para criar 10 pesos aleatórios.

peso = np.random.random(num_assets)
peso /= np.sum(peso)
peso
np.sum(peso)
for single_portfolio in range(num_portfolios):
weights = np.random.random(num_assets)
weights /= np.sum(weights)
returns = np.dot(weights, retorno_anual)
volatility = np.sqrt(np.dot(weights.T, np.dot(cov_anual, weights)))
port_returns.append(returns)
port_volatility.append(volatility)
stock_weights.append(weights)
portfolio = {'Retornos': port_returns, 'Volatilidade': port_volatility}
for counter,symbol in enumerate(ativos):
portfolio[symbol+' peso'] = [weight[counter] for weight in stock_weights]
df = pd.DataFrame(portfolio)
df.head()
retornos = df.sort_values(by = ['Retornos'], ascending = False)
retornos.head()
plt.style.use('seaborn')

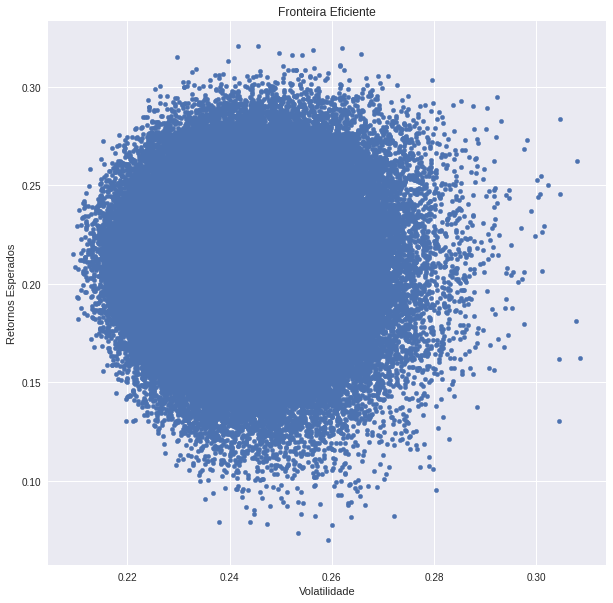
df.plot.scatter(x = 'Volatilidade', y = 'Retornos', figsize = (10,10), grid = True)

plt.xlabel('Volatilidade')

plt.ylabel('Retornos Esperados')

plt.title('Fronteira Eficiente')

plt.show()

retorno_max = retornos.iloc[:1]
retorno_max = retorno_max.drop(['Retornos', 'Volatilidade'], axis = 1)
retorno_max
pesos = np.array(retorno_max)
pesos
retorno_carteira = retorno_diario*pesos

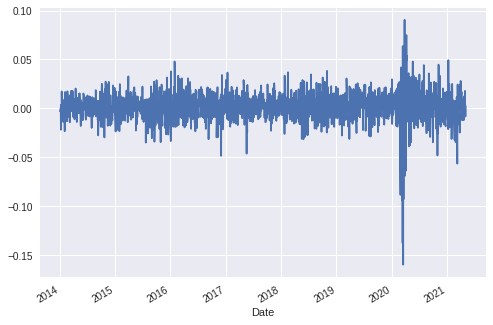
Plotando o retorno da carteira.

retorno_carteira.plot()

Retorno acumulado.

returns_acm = (1 + retorno_carteira).cumprod()
returns_acm.plot()

Importando dados do IBOV para Benchmark.

ibov = wb.DataReader('^BVSP', data_source = 'yahoo', start = '2014-01-01', end = '2021-05-03')['Adj Close']
type(ibov)
pandas.core.series.Series
ibov_retornos = ibov.pct_change()
ibov_retornos_acm = (1 + ibov_retornos).cumprod()
pd.DataFrame(ibov_retornos_acm)
novo_df = pd.merge(pd.DataFrame(ibov_retornos_acm), pd.DataFrame(returns_acm, columns = ['Minha Carteira']), how = 'inner', on = 'Date')
novo_df.rename(columns = {'Adj Close': 'IBOV'}, inplace = True)
novo_df.head()
novo_df.plot()

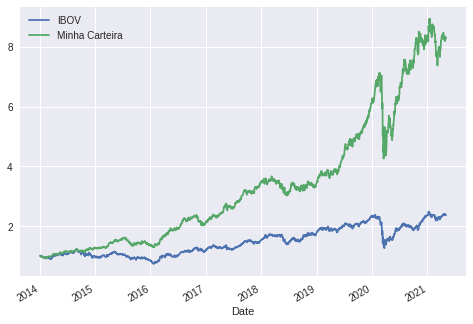
Podemos observar que a carteira estimada pela fronteira eficiente teve um desempenho melhor que a carteira de mercado, que no caso do estudo foi o Ibovespa.