Esse é um post rápido para comparar os resultados de duas técnicas de matching diferentes: Propensity-score matching (PSM) e Entropy matching.

Uma explicação mais apurada das técnicas está fora do escopo desse post, mas de uma forma simples, você pode pensar da seguinte forma.

Propensity-score matching (PSM) faz o pareamento entre unidades do grupo de controle e tratamento com base na propensão de se receber o tratamento dado um conjunto de covariates.

Propensity-score é simplesmente um número que indica a probabilidade de se receber o tratamento.

Assim, o pareamento com base em propensity-score é simplesmente o pareamento usando essa probabilidade como critério fundamental.

Entropy matching, por sua vez, faz o pareamento com base em um ou mais momentos da distribuição dos covariates.

Basicamente, você usa como critério de pareamento: a média (1º momento), variância (2º momento), skewness (3º momento)…

O resultado é uma sub-amostra rebalanceada tal que os momentos dos covariates dos grupos de controle e tratamento são semelhantes.

De novo, essa é uma explicação curta, apenas para entendermos o básico das diferenças entre os dois métodos.

Vamos agora à estimação. Dessa vez, vou utilizar o Stata. Esse código é amplamente baseado nesse artigo.

Se você quiser o do-file utilizado, pode baixar aqui.

PSM

Instale os pacotes “psmatch2” e “ebalance” e carregue a seguinte base (a base estará disponível após instalar o pacote):

ssc install ebalance, all replace
use cps1re74.dta, clear

Vamos começar analisando os covariates “age”, “black” e “educ” no grupo de controle e no de tratamento. A variável de tratamento é “treat”.

Ao todo, temos 185 obs. de tratamento e 15,992 observações de controle.

qui estpost tabstat age black educ , by(treat) c(s) s(me v sk n) nototal
esttab . 	,varwidth(20) cells("mean(fmt(3)) variance(fmt(3)) skewness(fmt(3)) count(fmt(0))") noobs nonumber compress 

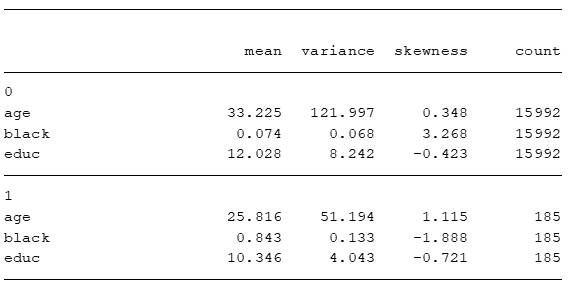
Claramente, os dois grupos são diferentes entre si. O grupo de tratamento é 1) mais jovem, 2) majoritariamente black, e 3) menos escolarizados que o grupo de controle.

Note também que a variância e skewness das duas sub-amostras são consideravelmente diferentes.

Se usássemos essas duas sub-amostras em alguma análise econométrica sem um pré-processamento para torná-las comparáveis, teríamos provavelmente coeficientes viesados por selection bias.

Assim, é importante executarmos algum método de pareamento para que eventuais análises futuras não sofram desse viés.

Vamos começar pelo PSM usando o pacote psmatch2. Vamos usar o pareamento mais simples, isto é, sem usar nenhuma função adicional.

Há várias funções e critérios distintos que você pode utilizar (e.g., definindo commom support, diferentes estimadores, etc.) que podem melhorar seu pareamento.

Mas, para fins desse exercício, vamos tomar o caminho mais simples e executar pareamento via Kernel, usando o default que é Epanechnikov kernel.

Faça o pareamento da seguinte forma:

psmatch2 treat age black educ , kernel

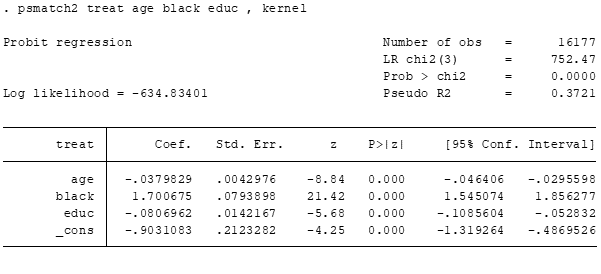
Após o pareamento, note que diversas variáveis foram criadas com um “_” no início de seus nomes.

A que mais nos importa é _weight que é o peso para rebalanceamento de cada observação.

Veja que o peso de cada observação varia entre [0,1]. Basicamente, quanto maior o peso, maior a similaridade entre a observação do grupo de tratamento e a de controle.

Pesos baixos indicam que a observação de controle é diferente da observação do grupo de tratamento.

Perceba também que as observações do grupo de tratamento tem peso 1, enquanto as demais (i.e., as de controle) tem pesos menores que 1.

bys treat: sum _weight , d

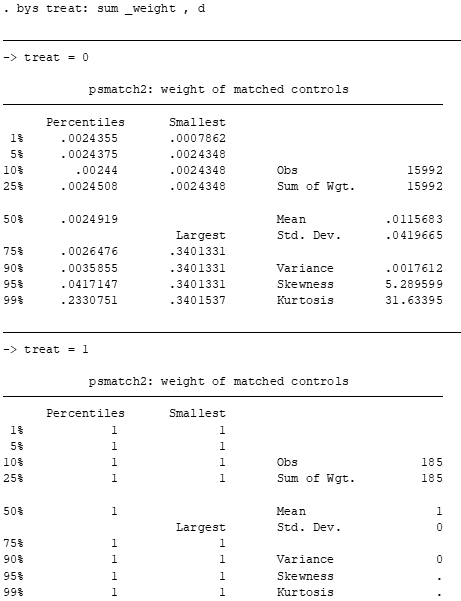
Podemos agora calcular a média, variância e skewness das amostras pareadas.

qui estpost tabstat age black educ [aweight = _weight], by(treat) c(s) s(me v sk n) nototal
esttab . 	,varwidth(20) cells("mean(fmt(3)) variance(fmt(3)) skewness(fmt(3)) count(fmt(0))") noobs  nonumber compress 

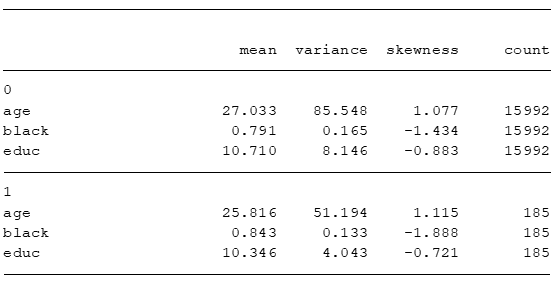
Perceba que, de acordo com esse pareamento, os três momentos não parecem semelhantes.

Não sabemos se as diferenças são estatisticamente significativas, mas visualmente, temos a impressão que sim na maioria dos casos.

Podemos fazer um teste da diferença entre as médias dos dois grupos via OLS da seguinte forma:

reg age   treat [aweight = _weight]
reg black treat [aweight = _weight]
reg educ  treat [aweight = _weight]

Perceba que todos os coeficientes da variável independente “treat” são estatisticamente diferentes de zero, ou seja, as diferenças entre as médias dos grupos são significativas.

Isso seria um indicativo que esse pareamento não cumpriu plenamente seu propósito de deixar as sub-amostras comparáveis.

É claro que fizemos o pareamento mais simples e eventualmente poderíamos melhorá-lo. No entanto, nesse momento, temos a sugestão de que as sub-amostras não foram bem pareadas.

Entropy

Vamos agora rodar o pareamento via entropia. Vamos também usar a versão de pareamento mais simples. Vamos apenas solicitar que os três momentos sejam usados como critério para pareamento.

ebalance treat age black educ, targets(3)

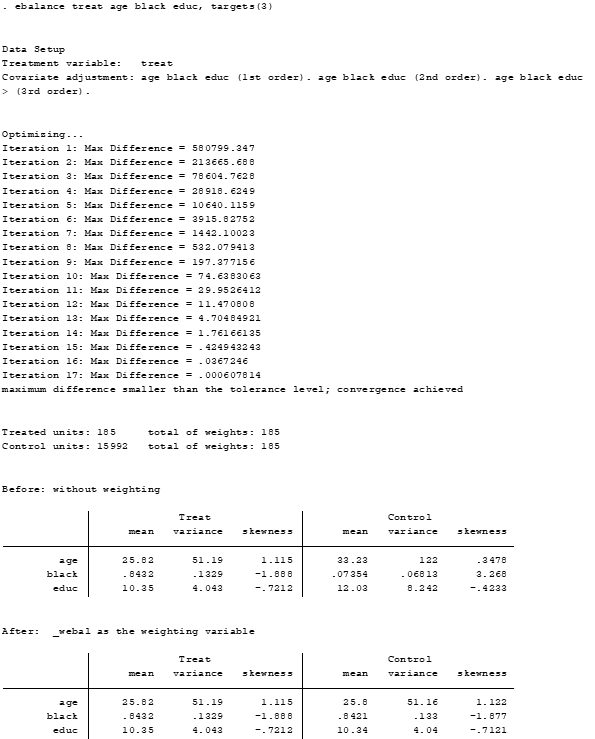
O próprio output da linha anterior mostra os momentos da distribuição dos dois grupos, mas se você quiser, pode rodar novamente as seguintes linhas:

qui estpost tabstat age black educ [aweight = _webal], by(treat) c(s) s(me v sk n) nototal
esttab . 	,varwidth(20) cells("mean(fmt(3)) variance(fmt(3)) skewness(fmt(3)) count(fmt(0))") noobs  nonumber compress 

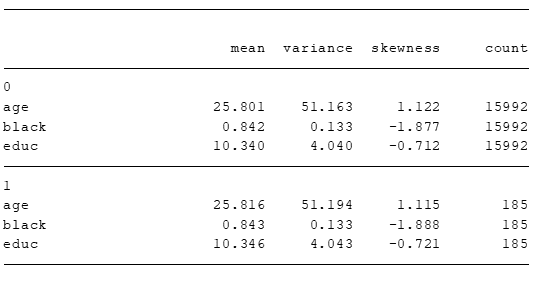
Vamos fazer o mesmo teste de averiguação de diferença de médias usando OLS.

reg age   treat [aweight = _webal]
reg black treat [aweight = _webal]
reg educ  treat [aweight = _webal]	

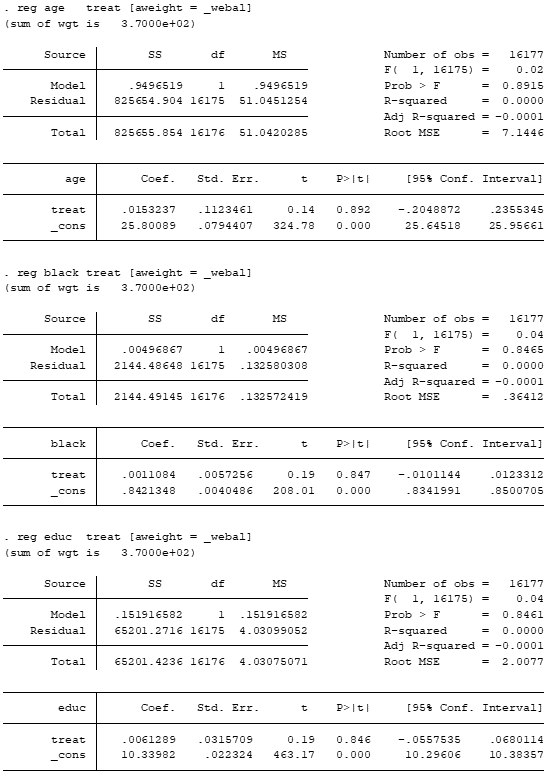
Note agora que os três coeficientes das variáveis independentes não são significativos.

Isso indica que as médias dos covariates entre os grupos não são estatisticamente diferentes entre si.

Conclusão

Ao que parece, o entropy matching é um método que leva a resultados mais apurados de pareamento.

É claro, esse foi um exercício simples. Mas para fins desse post, essa é a conclusão que conseguimos ter.

Thanks for passing by.