Cálculo do Beta de ativos usando o R

Nesse breve post, iremos calcular o Índice Beta de um ativo e plotar um gráfico com a dispersão dos retornos e a reta da regressão linear feita entre eles.

O Beta é uma medida de sensibilidade em relação a variações do seu benchmark. Seu cálculo é feito dividindo a covariância do ativo e seu benchmark pela variância do benchmark:

A equação acima é a mesma usada no cálculo do coeficiente angular de uma regressão linear simples, sendo conveniente utilizá-la na análise. Além disso, usá-la nos dá a vantagem de termos outros parâmetros/indicadores que podem nos ser úteis, como o coeficiente linear da regressão, que usaremos para plotar o gráfico, e o coeficiente de determinação ($R^2$), que nos diz quanto da variável dependente é explicado pela variável explicativa (nesse caso quanto das variações de um ativo são explicadas pelas variações do mercado).

Os valores do Beta podem ser interpretado como abaixo:

• $\beta$ > 1: Ativo mais volátil que o benchmark;

• $\beta$ = 1: Ativo tão volátil quanto o benchmark;

• 0 < $\beta$ < 1: Ativo menos volátil que o benchmark;

• $\beta$ < 0: Ativo inversamente correlacionado com o benchmark.

Faremos um exemplo através da regressão linear entre Petrobras PN (PETR4) e Ishares Ibovespa (BOVA11).

Começaremos importando os dados de preços do ativo e do benchmark e os transformando em retornos diários. Após isso, criamos um novo dataframe com ambos os retornos e realizamos uma regressão linear entre os pontos de dados nas colunas de retornos. Após isso separamos os dados de interesse e criamos uma mensagem para armazená-los. No final elaboramos um gráfico de dispersão e linha de regressão dos retornos.

Importando as bibliotecas necessárias.

library(tidyquant) # Usado para importação e manipulação dos dados.
library(dplyr) # Usado para manipulação dos dados.
library(ggplot2) # Usado para a elaboração de gráficos.

Importando os dados de preço dos ativos.

# Para calcular o beta precisaremos de um benchmark e uma ação. Usaremos como benchmark o BOVA11 e como ação a PETR4.
# Observação: como os dados são obtidos do Yahoo Finance, temos que usar o ticker utilizado por ele. Nesse caso, foi necessário colocar o '.SA' após o ticker usual dos ativos, por serem ativos Sul-Americanos (South Americans).

bmk = "BOVA11.SA"
ativo = "PETR4.SA"
inicio = "2015-01-01"

# Usaremos a função tq_get() da biblioteca tidyquant para importar os dados de preço dos ativos escolhidos.

Rb = tq_get(bmk,
            from = inicio,
            to = as.character(Sys.Date()),
            get = "stock.prices")

Ra = tq_get(ativo,
            from = inicio,
            to = as.character(Sys.Date()),
            get = "stock.prices")

Manipulando os dados para se obter os retornos diários.

# Selecionamos apenas os dados de preço de fechamento ajustados por dividendos e desdobramentos (coluna 'adjusted') e transformamos em retornos.

Rb = Rb %>%
  tq_transmute(select     = adjusted, 
              mutate_fun = dailyReturn, 
              col_rename = "Rb")

Ra = Ra %>%
  tq_transmute(select     = adjusted, 
              mutate_fun = periodReturn, 
              period     = "daily", 
              col_rename = "Ra")

Consolidando os dados em um único dataframe.

# Criamos um novo dataframe com as colunas de interesse, unindo a partir dos valores de data.

port = full_join(Ra, 
                Rb,
                by = "date")

Realizando uma regressão linear entre os retornos dos ativos para obter o Beta ($\beta$) e o Coeficiente de Determinação ($R^2$).

reg = lm(Ra~Rb, data = port)

# Guardamos as informações de interesse para posterior uso.

intercepto = round(reg$coefficients[1], 2)
beta = round(reg$coefficients[2], 2)
R.squared = round(summary(reg)$adj.r.squared, 2)

Manipulando o nome dos ativos para retirar a extensão “.SA” do final dos tickers.

ativo = strsplit(ativo, ".", fixed = T)[[1]][1]
bmk = strsplit(bmk, ".", fixed = T)[[1]][1]

Elaborando uma mensagem com as informações de interesse da regressão.

msg = paste0(ativo,'=',intercepto,'+', beta,'*', bmk, '\n',
            'Adj. R-squared = ', R.squared, '\n',
            'Beta = ', beta)

Imprimindo a mensagem com as informações de interesse.

cat(msg)

Elaborando um gráfico de dispersão com os dados de interesse e linha de regressão.

# Visando evitar conflitos posicionais entre os dados e a mensagem no gráfico, utilizamos uma estrutura condicional para determinar a localização da mensagem de acordo com a inclinação da reta de regressão linear.

if(beta >= 0){
  
  # Caso o beta seja positivo (a reta tenha inclinação positiva), a mensagem ficará posicionada no canto superior esquerdo do gráfico.

  x.pos = min(port$Rb)+(max(port$Rb)-min(port$Rb))/6
  y.pos = max(port$Ra)-(max(port$Ra)-min(port$Ra))/6
  
} else {
  
  # Caso o beta seja negativo (a reta tenha inclinação negativa), a mensagem ficará posicionada no canto superior direito do gráfico.

  x.pos = max(port$Rb)-(max(port$Rb)-min(port$Rb))/6
  y.pos = max(port$Ra)-(max(port$Ra)-min(port$Ra))/6
  
}

# Plotamos efetivamente os dados usando a biblioteca ggplot2.

ggplot(data = port, aes(x=Rb, y=Ra)) +
  geom_point() +
  geom_smooth(method = lm, se = F, color = 'dodgerblue3')+
  theme_light() +
  labs(x = paste('Retorno', bmk),
       y = paste('Retorno', ativo),
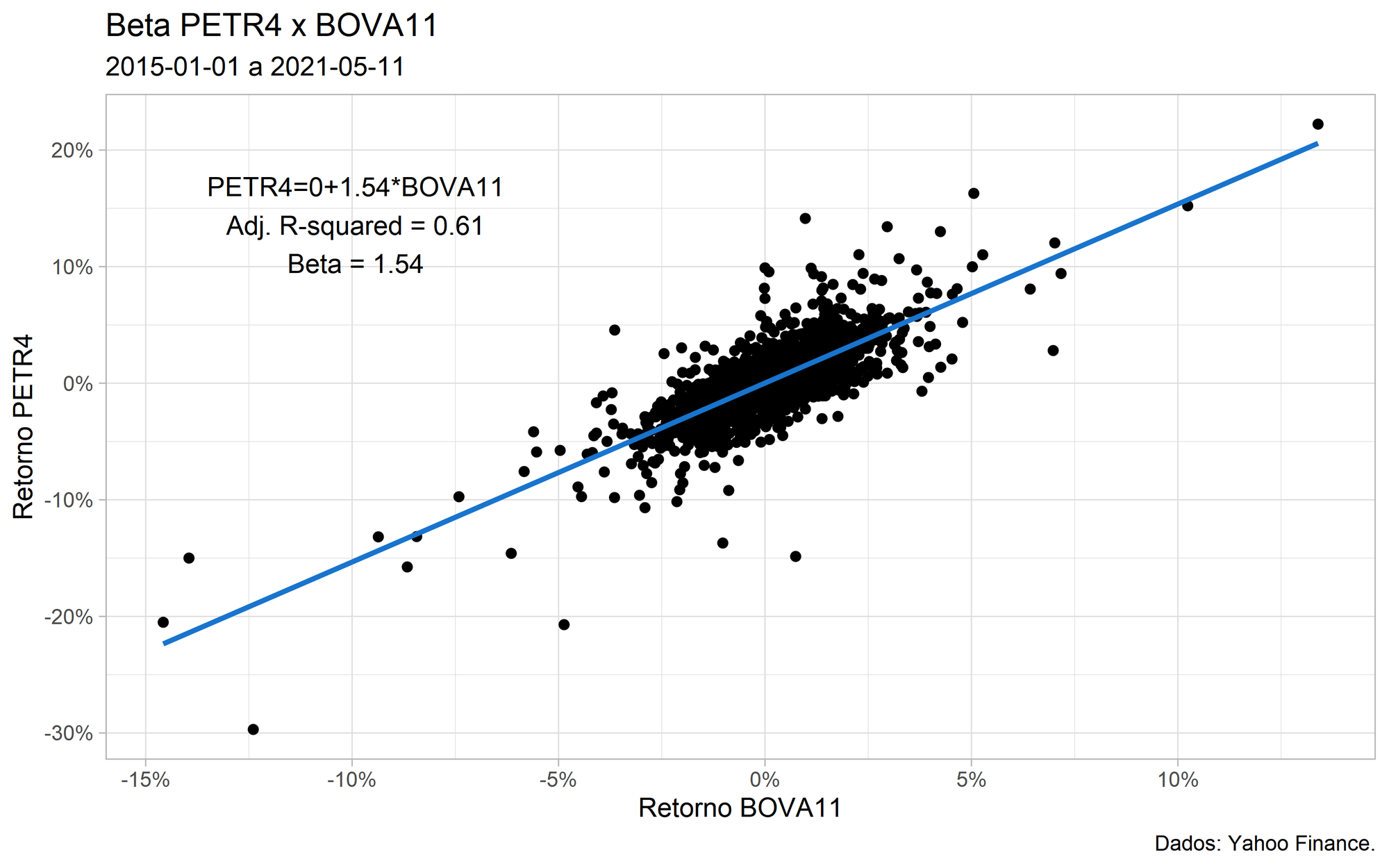
       title = paste("Beta", ativo, 'x', bmk),
       subtitle = paste(inicio, 'a', as.character(Sys.Date())),
       caption = "Dados: Yahoo Finance.") +
  scale_x_continuous(labels = function(x) paste0(100*x, "%"))+
  scale_y_continuous(labels = function(x) paste0(100*x, "%"))+
  annotate('text', label = msg, x = x.pos, y = y.pos)

A partir dos resultados obtidos na análise, podemos observar que a PETR4 é mais volátil que o mercado em geral ($\beta > 1$), já que seu beta é de 1.54. Vemos também que o seu $R^2$ é 0.61, ou seja, em média, 61% da variação dos retornos diários de PETR4 podem ser explicadas pela variação nos retornos diários do BOVA11.

O processo acima pode ser consolidado em uma função de fácil utilização.

# A função tem como parâmetros o ativo de interesse, o ativo a ser utilizado de benchmark para o cálculo do Beta, a data inicial dos dados e um valor booleano que indicará se haverá a elaboração de um gráfico ou apenas a impressão de uma mensagem com as informações de interesse.

calculo.beta = function(ativo, bmk, inicio, plot){

  Rb = tq_get(bmk,
              from = inicio,
              to = as.character(Sys.Date()),
              get = "stock.prices")
  
  Ra = tq_get(ativo,
              from = inicio,
              to = as.character(Sys.Date()),
              get = "stock.prices")
  
  Rb = Rb %>%
    tq_transmute(select     = adjusted, 
                mutate_fun = dailyReturn, 
                col_rename = "Rb")
  
  Ra = Ra %>%
    tq_transmute(select     = adjusted, 
                mutate_fun = periodReturn, 
                period     = "daily", 
                col_rename = "Ra")
  
  port = full_join(Ra, 
                  Rb,
                  by = "date")
  
  reg = lm(Ra~Rb, data = port)
  
  intercepto = round(reg$coefficients[1], 2)
  beta = round(reg$coefficients[2], 2)
  R.squared = round(summary(reg)$adj.r.squared, 2)
  
  ativo = strsplit(ativo, ".", fixed = T)[[1]][1]
  bmk = strsplit(bmk, ".", fixed = T)[[1]][1]
  
  msg = paste0(ativo,'=',intercepto,'+',beta,'*',bmk, '\n',
              'Adj. R-squared = ', R.squared, '\n',
              'Beta = ',beta)
  
  if (plot == T) {
    
    if(beta >= 0){
      
      x.pos = min(port$Rb)+(max(port$Rb)-min(port$Rb))/6
      y.pos = max(port$Ra)-(max(port$Ra)-min(port$Ra))/6
      
    } else {
      
      x.pos = max(port$Rb)-(max(port$Rb)-min(port$Rb))/6
      y.pos = max(port$Ra)-(max(port$Ra)-min(port$Ra))/6
      
    }

    ggplot(data = port, aes(x=Rb, y=Ra)) +
      geom_point() +
      geom_smooth(method = lm, se = F, color = 'dodgerblue3')+
      theme_light() +
      labs(x = paste('Retorno', bmk),
          y = paste('Retorno', ativo),
          title = paste("Beta", ativo, 'x', bmk),
          subtitle = paste(inicio, 'a', as.character(Sys.Date())),
          caption = "Dados: Yahoo Finance.") +
      scale_x_continuous(labels = function(x) paste0(100*x, "%"))+
      scale_y_continuous(labels = function(x) paste0(100*x, "%"))+
      annotate('text', label = msg, x = x.pos, y = y.pos)

  } else {
    
    cat(msg)

  }
}

calculo.beta(ativo = 'PETR4.SA', bmk = 'BOVA11.SA', inicio = '2015-01-01', plot = TRUE)