Introdução

A motivação desse post é mostrar como implementar, em R, dois modelos básicos e instrutivos em simulações estocásticas. São eles,

• Passeio Aleatório: modelo que serve como base para diversos processos estocásticos e cuja equação discreta é dada por,

\begin{align} S_{t} = S_{t-1}+e_{t},\end{align}

onde $S_t$ é o saldo acumulado no instante $t$ e $e_{t}$ é o ganho/perda no instante $t$.

• Binomial: modelo de discretização do movimento geométrico browniano com ótima performance computacional e cuja equação discreta é dada por,

\begin{align} S_{t} = S_{t-1}\times e_{t},\end{align}

onde $S_t$ é o valor da varável aleatória no instante $t$ e $e_{t}$ é um fator de subida ($e_{t}>1$) ou um fator de descida ($0<e_{t}<1$) no instante $t$.

Descrição do algoritmo

Carregando os parâmetros: fator de subida (xp), fator de descida (xm), valor inicial (S0), probabilidade de subida (pp), probabilidade de descida (pm), número de passos (n) e número de caminhos a serem plotados em cada simulação (path).

xp <- 1.1; xm <- 0.9         
S0 <- 0.5                   
pp <- 0.6; pm <- 1-pp        
n <- 100                    
path <- 10

Construindo o vetor do valor acumulado a cada passo. Aqui basta escolher qual modelo quer simular, passeio aleatório (processo aditivo) ou o modelo binomial (processo multiplicativo). No exemplo abaixo, estamos rodando o modelo binomial.

a <- runif(n, min = 0, max = 1)                    
e <- matrix(nrow = 1, ncol = n-1, NA)               
S <- matrix(nrow = 1, ncol = n, NA); S[1] <- S0

Construindo o vetor de ganho/perda.

for (i in 1:(n-1)) {
  if (a[i]>pp) e[i] <- xm else e[i] <- xp           
}

Construindo o vetor do valor acumulado a cada passo. Aqui basta escolher qual modelo quer simular, passeio aleatório (processo aditivo) ou o modelo binomial (processo multiplicativo). No código abaixo, estamos rodando o modelo binomial.

for (i in 2:n) {
    #S[i] <- S[i-1]+e[i-1]                         
    S[i] <- S[i-1]*e[i-1]                          
}

Plotando o primeiro caminho.

plot(c(1:n), S, type = "l", xlab = "n", ylab = "S", xlim = c(0,n), ylim = c(min(S),max(S)))

Construindo e plotando os demais caminhos. Aqui também pode-se escolher entre os dois modelos.

for (j in 1:path) {                                 # building different paths
  a <- runif(n, min = 0, max = 1)
  S[1] <- S0

  for (i in 1:(n-1)) {
    if (a[i]>pp) e[i] <- xm else e[i] <- xp
  }
  for (i in 2:n) {
    #S[i] <- S[i-1]+e[i-1]                          # S for Random Walk
    S[i] <- S[i-1]*e[i-1]                            # S for Binomial Model
  }
  lines(c(1:n), S, type = "l", col = j)            
}

Output do código

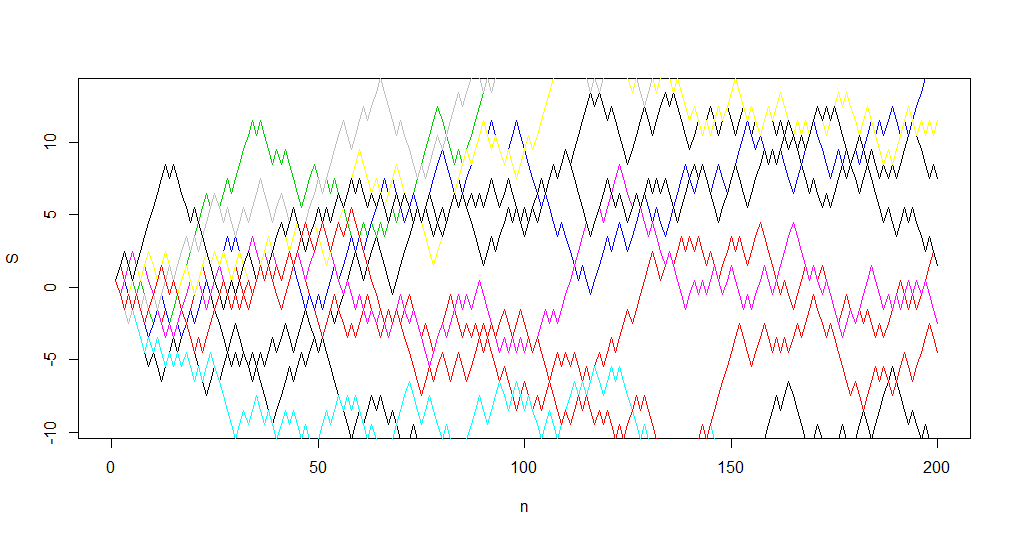
A figura abaixo representa um exemplo de simulação com 10 caminhos possíveis e 200 passos para o Passeio Aleatório. A figura foi gerada com a seguinte seed:

xp <- 1; xm <- -1         
S0 <- 0.5                    
pp <- 0.5; pm <- 1-pp        
n <- 200                     
path <- 10 

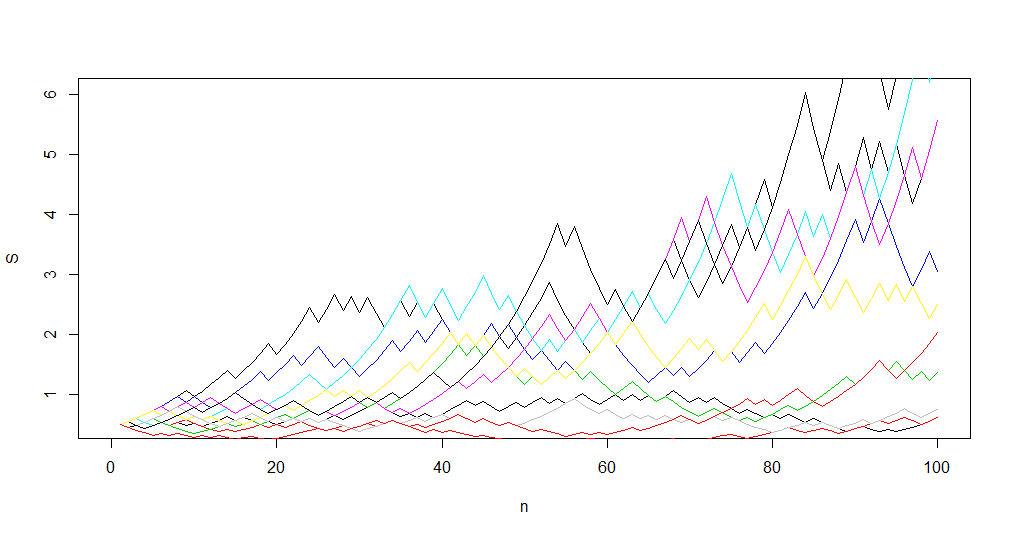
Nossa próxima figura representa um exemplo de simulação com 10 caminhos possíveis e 100 passos para o Modelo Binomial. A figura foi gerada com a seguinte seed:

xp <- 1.1; xm <- 0.9        
S0 <- 0.5                   
pp <- 0.6; pm <- 1-pp       
n <- 100                    
path <- 10  

É importante notar que o vetor de probabilidades (a) é gerado aleatoriamente com uma distribuição uniforme. Isso significa que as seeds sugeridas anteriormente, resultaram em gráficos semelhantes aos apresentados neste post, mas não exatamente iguais a eles.

Alterando os parâmetros dos modelos, podemos construir simulações com tendências de subida, por exemplo, utilizando pp <- 0.8. Um bom exercício é modificar os parâmetros e plotar os gráficos para entender como cada parâmetro influencia cada modelo.