Erros padrão robustos e clusterização dos erros padrão

Nesse breve post apresento uma rápida discussão sobre erros robustos e clusterização dos erros padrão, além de apresentar como é possível implementar essas soluções em regressões no R. O uso dessas diferentes estratégias para computar os erros padrão é uma importante decisão de desenho de pesquisa frequentemente discutida por avaliadores em journals ou em congressos e, ao menos pela minha breve experiência, é um tratamento usualmente necessário, ao menos na pesquisa em contabilidade e finanças. Mas, antes de partirmos direto para a implementação dessas soluções, devemos antes saber: quando isso será necessário? De forma geral, você deverá pensar nisso – ou já deve estar pensando nisso – quando o termo de erro no seu modelo linear não tem um comportamento homocedástico (o Ben Lambert faz uma boa revisão sobre homoscedasticidade e heterocedasticidade aqui: https://bit.ly/3u4K3L3).

Embora não provoque viés nos coeficientes em si, a heterocedasticidade pode arruinar os resultados de uma pesquisa a partir do momento que induz viés nos erros padrão dos coeficientes, podendo resultar em inferências inadequadas. Os erros de uma regressão representam o quão longe está da reta de regressão. Idealmente, os dados devem ser homocedásticos, isso é, esse erro deve seguir uma variância constante e, visualmente, deveríamos observar erros com um comportamento uniforme próximo a reta da regressão estimada, sem grande dispersão.

A heterocedasticidade surge pela natureza dos dados. Hipoteticamente, imagine um modelo de regressão onde a renda é explicada pela idade. O racional por trás desse modelo é ingenuamente simples: quanto mais velho você é, maior a sua renda. De forma geral podemos deduzir que a maior parte dos adolescentes e jovens adultos recebem algo não muito acima do salário mínimo. Digamos, então, que até os 25 anos não existe muita variabilidade nos dados. Depois dos 30 anos, entretanto, as diferenças costumam a aparecer com mais frequência: alguns podem ter alcançado o cargo de sênior e aumentado o salário em dez vezes enquanto outros podem ter, no máximo, dobrado o salário. A intuição aqui é de que a variabilidade do salário tenderá a aumentar conforme a idade e isso, muito provavelmente, incorreria em problemas de heterocedasticidade: isso é, os erros não seriam homocedásticos – o erro em torno da reta de regressão aumentaria conforme a idade, dado a maior variabilidade. Para identificar formalmente a existência de problemas de heterocedasticidade existem inúmeros testes, que não vou discutir aqui. Entretanto, entre esses testes, o teste de Breusch Pagan já é um bom começo.

Intuição à parte, apresentamos a seguir quais são as possíveis formas de implementar tratamentos para esse tipo de problema. Discutirei em duas partes: i) erros padrão robustos, tratamento “clássico” para a heterocedasticidade e; ii) clusterização dos erros padrão, caso especial de erros padrão robustos utilizados para casos mais particulares.

Primeiro devemos carregar uma base de dados. Nesse exemplo, utilizarei uma base de dados disponibilizada no próprio R com mais de duas variáveis. Para treinar, você pode usar uma base de dados própria ou alguma outra que seja de fácil acesso. Não iremos partir para a interpretação das relações estimadas. Usaremos os seguintes pacotes a seguir: fixest e sandwich. Lembrando que é possível aplicar as correções tratadas a seguir usando o plm + a função coeftest, mas o caminho é diferente e isso acabaria ficando melhor explicado em outro post.

    #Carregando alguns pacotes e o primeiro conjunto de dados que iremos utilizar para o exemplo 
    library(fixest)
    library(sandwich)
    data(iris)
    datairis <- iris

Em seguida, estimaremos um modelo de regressão OLS (Ordinary Least Squares) com efeitos fixos por meio da função feols, parte do pacote fixest. No exemplo, iremos regredir dois modelos simples: i) Petal.Lenght contra Petal.Width e; ii) o mesmo modelo anterior, mas com mais uma variável, Sepal.Width.

    #Estimando modelos  de regressão
    modelo1 <- feols(Petal.Length  ~ Petal.Width, data = datairis)
    modelo2 <- feols(Petal.Length  ~ Petal.Width + Sepal.Width, data = datairis)

Erros padrão robustos. Para verificar as estimações dos modelos anteriores com os erros padrão sem levar em consideração ajustes para problemas de heterocedasticidade, basta especificar “standard” no comando exibido a seguir. A função etable do fixest permite visualizar os resultados de duas ou mais diferentes estimações simultaneamente. Em “S.E. type” é possível verificar o tratamento dado ao erro padrão e, como esperado, verificamos erros calculados da forma padrão, sem tratamento para possíveis problemas de heterocedasticidade ou emprego de clusterização.

etable(modelo1, modelo2, se = "standard")

Como o nosso interesse é tratar possíveis problemas de heterocedasticidade, nós substituiremos o “standard” apresentado anteriormente por “hetero”. Dessa forma, computaremos erros padrão robustos a heterocedasticidade, mais especificamente na forma mais “tradicional” de se tratar problemas de heterocedasticidade (emprego de HC1), que pode ser vista em detalhes aqui: https://data.library.virginia.edu/understanding-robust-standard-errors/.

Entretanto, como veremos mais na frente, existem outras formas de computar erros padrão robustos a heterocedasticidade (HC2, HC3, entre outras, que se diferenciam pela forma de se calcular). Como é possível observar na imagem a seguir, em “S.E. Type” é apontado que os erros-padrão dos modelos estimados são robustos a heterocedasticidade. Como devem perceber, a grande diferença entre os modelos estimados na imagem anterior e os modelos estimados na imagem a seguir não está nos coeficientes, que permanecem idênticos. A única (e importante) mudança esteve nos valores dos erros-padrão, agora menos enviesados, sob a premissa de que os dados não são homocedásticos.

etable(modelo1, modelo2, se = "hetero")

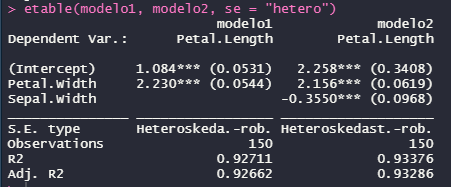
É importante destacar que a correção “hetero” é baseada no HC1 Robust Standard Error, que não é idêntica a correção de White mais conhecida, que é baseada na HC3, padrão do pacote sandwich. É possível empregar as diferentes variações de tratamentos dos erros padrão, como a correção clássica de White (H0), a correção de Mackinnon e White (HC2) ou a correção de Cribari-Neto (HC4). Como podem perceber, há situações em que diferentes correções não implicam em diferenças perceptíveis nos erros padrão observados. Por essa razão, não vou reportar as imagens dos testes a seguir por brevidade.

    #Correção clássica de White
    etable(modelo1, modelo2, .vcov = sandwich::vcovHC, .vcov.args = list(type = "HC0"))
    #Correção de Mackinnon e White
    etable(modelo1, modelo2, .vcov = sandwich::vcovHC, .vcov.args = list(type = "HC2"))
    #Correção de Cribari-Neto
    etable(modelo1, modelo2, .vcov = sandwich::vcovHC, .vcov.args = list(type = "HC4"))

Com pequenas modificações é possível estimar alguns tratamentos mais complexos, como a correção de Newey-West que, teoricamente, procura resolver problemas de heterocedasticidade e correlação serial.

    #Correção de Newey-West
    etable(modelo1, modelo2, .vcov = sandwich::NeweyWest, .vcov.args = list(type = "NeweyWest"))

Clusterização dos erros padrão, caso especial de erros padrão robustos que leva em conta a heterocedasticidade entre clusters das observações. Em algumas situações mais particulares, clusterizar os erros-padrão pode ser necessário. Em algumas situações ainda mais particulares, pode ser interessante clusterizar os erros padrão em mais de uma maneira (two-way, three-way, e por aí vai…). Em um trabalho recente, onde os dados eram infestados por problemas de correlação serial, me foi indicado clusterizar os dados em two-way. Como eu poderia clusterizar em one-way? E como clusterizar em two-way? Pelo fixest não é complicado. É necessário apenas especificar se os erros-padrão serão clusterizados por meio de um cluster único (“cluster”) ou por mais de um cluster (“twoway”), especificando o nível da clusterização.

Para o exemplo a seguir, vamos precisar carregar a seguinte base de dados.

    #Carregando dados
    data(airquality)
    dataair <- airquality

Em seguida, estimamos os modelos de regressão.

    #Estimando modelos de regressão
    modelo3 <- feols(Ozone  ~ Solar.R, data = dataair)
    modelo4 <- feols(Ozone  ~ Solar.R + Wind, data = dataair)

Para clusterizar os erros-padrão em one-way, devemos especificar o cluster. No exemplo a seguir o cluster será feito com base no mês.

    # Clusterizando em one-way (one-way clustering)
    etable(modelo3, modelo4, se = "cluster", cluster =c("Month"))

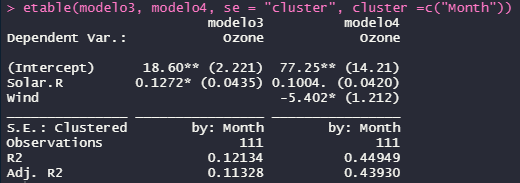
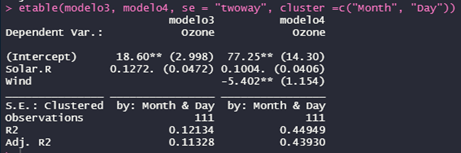
Para clusterizar os erros-padrão em dois níveis, devemos especificar que desejamos estimar os erros-padrão em twoway e, em seguida, especificar os dois níveis de clusters a serem empregados. No exemplo a seguir empregamos Mês e Dia.

    #Clusterizando em two-way (two-way clustering) 
    etable(modelo3, modelo4, se = "twoway", cluster =c("Month", "Day"))