Funções de Resposta ao Impulso para a Produção Industrial com relação a choques na taxa Selic
Motivação
A taxa Selic se encontra em níveis extremamente baixos, caracterizando um nível de estímulo monetário que tem colocado em risco o cumprimento das metas de inflação no horizonte relevante para a política monetária do Banco Central do Brasil (BCB). Sendo assim, como indicado nas últimas atas do COPOM (veja @ataBCB2021Marco e @ataBCB2021Maio), haverá um processo de normalização da taxa de juros nos próximos meses, o que poderá gerar impactos em termos de reação da indústria. Com isso, iremos estimar Funções de Resposta ao Impulso derivadas de Modelos de Correção de Erros Vetorial (VEC) para analisar qual seria a reação da produção industrial a um choque ortogonal na taxa Selic.
Serão analisados os seguintes segmentos da produção industrial:
- Indústria geral
- Indústrias extrativas
- Indústrias de transformação
- Produção de bens de capital
- Produção de bens intermediários
- Produção de bens duráveis
- Produção de bens não duráveis
As bibliotecas necessárias são:
library(tidyverse)
library(lubridate)
library(seasonal) # dessazonalização
library(readxl) # leitura de excel
library(sidrar) # dados do IBGE
library(ipeadatar) # dados do ipeadata
library(rbcb) # dados do BCB. Este pacote não está disponível no CRAN, para instalar use devtools::install_github('wilsonfreitas/rbcb')
library(fredr) # dados do FRED
library(urca) # testes de raiz unitária e cointegração
library(vars) # modelagem de VAR
library(gridExtra) # juntar gráficos em um grid
Tema padrão para os gráficos:
theme_set(theme_classic())
theme_update(panel.grid.major.y = element_line(linetype = "dotted", color = "gray70"),
axis.title = element_text(size = 9, color = "black"),
axis.text = element_text(size = 8, color = "black"),
plot.title = element_text(size = 12, color = 'black'),
plot.caption = element_text(size = 13, color = 'black'),
plot.subtitle = element_text(size = 13, color = 'black'))
Dados
Variáveis utilizadas
Com base na literatura de maior referência para este tipo de estudo (veja @bernanke1992, @evans1996, e @bernanke1998) e uma referência que faz um estudo similar para outros países (veja @dedola2005), serão utilizadas as seguintes variáveis para compôr o vetor de variáveis endógenas:
- Taxa de juros de curto prazo (média mensal da Selic diária)
- Produção industrial (PIM-PF)
- Inflação mensal (variação mensal do IPCA)
- Taxa de câmbio (média mensal da taxa de câmbio R$/U$D, em ln)
- Agregado monetário (Meios de pagamento - M1, em ln)
- Concessões de crédito (em ln)
Além disso, também serão consideradas as seguintes variáveis exógenas:
- Taxa de juros dos EUA (fedfunds)
- Índice de preços global de commodities (em ln)
- Medida de risco país para o Brasil (EMBI+, em ln)
- Indicadora de recessão para o Brasil
Os dados utilizados terão peridiocidade mensal, com início em 2002-01-01 e fim em 2021-03-01.
Baixando os dados
Com exceção da variável indicadora de recessão para o Brasil, todas as outras podem ser obtidas diretamente no R.
Taxa Selic (fonte: BCB):
code <- c(selic_daily = 1178)
juros_db <- rbcb::get_series(code, "2002-01-01") # baixa os dados do SGS do BCB
## Calculando a média mensal
juros <- juros_db %>%
mutate(month = month(date), year = year(date)) %>%
group_by(month, year) %>%
summarise(selic = mean(selic_daily)) %>%
mutate(day = 1, date = as.Date(paste(year, month, day, sep = "-"))) %>%
ungroup() %>%
dplyr::select(date, selic) %>%
arrange(date)
Produção industrial (fonte: IBGE):
## Bens de capital, Bens intermediários, bens de consumo duráveis, bens de consumo semiduráveis e não duráveis
pim_1 <-
'/t/3651/n1/all/v/3134/p/all/c543/129278,129283,129301,129305/d/v3134%201' %>%
get_sidra(api = .) %>%
dplyr::mutate(date = parse_date(`Mês (Código)`, format = '%Y%m')) %>%
dplyr::select(date, "Grandes categorias econômicas", Valor) %>%
pivot_wider(names_from = "Grandes categorias econômicas", values_from = Valor)
## Indústria geral, extrativa e transformação
pim_2 <-
'/t/3653/n1/all/v/3134/p/all/c544/129314,129315,129316/d/v3134%201' %>%
get_sidra(api = .) %>%
mutate(date = parse_date(`Mês (Código)`, format = '%Y%m')) %>%
dplyr::select(date, "Seções e atividades industriais (CNAE 2.0)", Valor) %>%
pivot_wider(names_from = "Seções e atividades industriais (CNAE 2.0)", values_from = Valor)
## Juntando em uma tabela
PIM <- left_join(pim_2, pim_1, by = "date") %>%
rename("Indústria geral" = "1 Indústria geral",
"Indústrias extrativas" = "2 Indústrias extrativas",
"Indústrias de transformação" = "3 Indústrias de transformação",
"Bens de capital" = "1 Bens de capital",
"Bens intermediários" = "2 Bens intermediários",
"Bens de consumo duráveis" = "31 Bens de consumo duráveis",
"Bens de consumo não duráveis" = "32 Bens de consumo semiduráveis e não duráveis")
Inflação (fonte: IBGE):
IPCA_SA <- get_sidra(api = "/t/118/n1/all/v/all/p/all/d/v306%202") %>%
mutate(date = parse_date(`Mês (Código)`, format = '%Y%m')) %>%
dplyr::select(date, IPCA_M = Valor) %>%
filter(date >= as.Date("2002-01-01"))
Taxa de câmbio (fonte: BCB):
code <- c(cambio = 3698)
usd <- rbcb::get_series(code, "2002-01-01") # baixa os dados do SGS do BCB
Agregado monetário (fonte: BCB):
code <- c(money_supply = 27841)
money <- rbcb::get_series(code, "2002-01-01") # baixa os dados do SGS do BCB
Concessões de crédito (aplicamos também o método X13-ARIMA-SEATS para dessazonalizar; fonte: BCB):
code <- c(credito = 21277)
credito <- rbcb::get_series(code, "2002-01-01") # baixa os dados do SGS do BCB
credito <- credito %>%
mutate(credito_sa = final(seas(ts(credito, start = c(2002, 1), frequency = 12)))) %>% # dessazonalização
dplyr::select(date, credito_sa)
credito$credito_sa <- as.numeric(credito$credito_sa)
FEDFUNDS (fonte: FRED): Para baixar os dados do FRED, é necessário especificar a chave do API. Veja como obter aqui.
fredr_set_key("1234567890abcdefg") # Insira aqui a sua chave do API do FRED
fedfunds <- fredr(
series_id = "FEDFUNDS",
observation_start = as.Date("2002-01-01"),
observation_end = as.Date("2021-03-01")
) %>%
dplyr::select(date, value) %>%
rename(fedfunds = value)
Índice de preços global de commodities (fonte: FMI, via FRED):
commodities <- fredr(
series_id = "PALLFNFINDEXM",
observation_start = as.Date("2002-01-01"),
observation_end = as.Date("2021-03-01")
) %>%
dplyr::select(date, value)%>%
rename(commodities = value)
Risco Brasil (fonte: JP Morgan, via ipeadata):
EMBI_db <- ipeadata("JPM366_EMBI366", quiet = FALSE) %>%
dplyr::select(date, value)
EMBI <- EMBI_db %>%
mutate(month = month(date), year = year(date)) %>%
group_by(month, year) %>%
summarise(EMBI = mean(value)) %>%
mutate(day = 1, date = as.Date(paste(year, month, day, sep = "-"))) %>%
ungroup() %>%
dplyr::select(date, EMBI) %>%
arrange(date) %>%
filter(date >= as.Date("2002-01-01"), date <= as.Date("2021-03-01"))
Indicadora de recessão para o Brasil (fonte: CODACE/FGV). Baixe o excel aqui:
dummy_recession <- read_excel("rececoes_codace.xlsx")
dummy_recession$date <- as.Date(dummy_recession$date)
dummy_recession <- dummy_recession %>%
filter(date >= as.Date("2002-01-01"))
Juntando os dados em uma tabela para as endógenas e uma para as exógenas:
db_industry <- left_join(PIM, juros, by = 'date') %>%
left_join(IPCA_SA, by = 'date') %>%
left_join(usd, by = 'date') %>%
left_join(credito, by = 'date') %>%
left_join(money, by = 'date') %>%
mutate(
log_money_supply = log(money_supply),
log_credito_sa = log(credito_sa),
log_cambio = log(cambio)
) %>% # transforma a inflação, crédito e M1 para ln
dplyr::select(-cambio, -credito_sa, -money_supply)
exogen <- as.matrix(cbind(dummy_recession[, 2],
fedfunds[, 2],
log(commodities[, 2]),
log(EMBI[, 2])))
Modelos
A mensuração dos efeitos da política monetária segue nos moldes de @dedola2005, sendo realizada em duas etapas. Primeiro é estimado um modelo mais geral, utilizando apenas a Produção Industrial Geral como variável de produção e as outras variáveis endógenas e exógenas. Na segunda etapa, incluímos a Produção Industrial Geral e mais uma variável de produção industrial em nível mais específico. Então, serão estimados no total sete modelos, sendo um deles contendo apenas a atividade em nível geral e o restante também contendo a atividade industrial em nível mais desagregado.
Nesse tipo de modelo a ordenação das variáveis endógenas no vetor importa, devendo ser feita com base no seu grau de exogeneidade. A ordenação adotada foi: nível de atividade, inflação mensal, taxa de juros de curto prazo, agregado monetário, concessões de crédito e taxa de câmbio. Para a etapa seguinte, a variável de atividade mais específica foi ordenada após o produto em nível mais geral.
Testes de raiz unitária
Para que um modelo do tipo VAR($p$) seja adequado, é necessário que este seja estacionário, implicando na necessidade de ausência de características que tornam o sistema de equações não-estacionário. Uma característica usual em séries econômicas que podem resultar na não-estacionariedade do sistema é a presença de tendência estocástica. Uma solução para isso seria levar em consideração as variáveis em sua primeira diferença, o que, na maioria dos casos, torna a série estacionária. Porém, ao aplicar essa transformação e construir um VAR em diferenças, informações importantes acerca de uma possível relação de longo prazo entre as séries acaba sendo descartada. Nesse sentido, um modelo do tipo VEC corrige este problema quando as séries em questão são não-estacionárias e cointegradas, ou seja, apresentam uma tendência estocástica em comum. Assim, um VEC faz com que seja possível analisar a dinâmica de curto e longo prazo entre as variáveis, em que, no curto prazo, os desvios da relação de longo prazo são corrigidos, e, no longo prazo, é considerada a relação de cointegração entre elas.
Então, primeiro vamos verificar se as séries em questão apresentam tendência estocástica a partir de testes de raiz unitária de @ADF1981, em que a hipótese nula do teste é que a série é não estacionária. Para isso, utilizamos a função ur.df do pacote urca:
summary(ur.df(db_industry$IPCA_M, type = 'drift', selectlags = "AIC", lags = 12))
summary(ur.df(db_industry$selic, type = 'trend', selectlags = "AIC", lags = 12))
summary(ur.df(db_industry$log_money_supply, type = 'trend', selectlags = "AIC", lags = 12))
summary(ur.df(db_industry$log_credito_sa, type = 'trend', selectlags = "AIC", lags = 12))
summary(ur.df(db_industry$log_cambio, type = 'trend', selectlags = "AIC", lags = 12))
summary(ur.df(db_industry$`Indústria geral`, type = 'drift', selectlags = "AIC", lags = 6))
summary(ur.df(db_industry$`Indústrias extrativas`, type = 'drift', selectlags = "AIC", lags = 6))
summary(ur.df(db_industry$`Indústrias de transformação`, type = 'drift', selectlags = "AIC", lags = 6))
summary(ur.df(db_industry$`Bens de capital`, type = 'drift', selectlags = "AIC", lags = 6))
summary(ur.df(db_industry$`Bens intermediários`, type = 'drift', selectlags = "AIC", lags = 6))
summary(ur.df(db_industry$`Bens de consumo duráveis`, type = 'drift', selectlags = "AIC", lags = 6))
summary(ur.df(db_industry$`Bens de consumo não duráveis`, type = 'drift', selectlags = "AIC", lags = 6))
Os testes não nos fornecem evidências para rejeitar a hipótese de presença de tendência estocástica em diversas das variáveis a 5% de significância (i.e. 95% de confiança), fazendo com que um VAR($p$) em níveis não seja adequado. Então, iremos verificar se há a existência de cointegração entre as variáveis, para que, então, possamos representar um VAR($p$) em nível por um VEC($p-1$), a partir do Teorema da Representação de @granger1987.
Definindo e estimando os modelos
O número de defasagens utilizado em um modelo do tipo VEC vem do número de defasagens utilizada no VAR em nível, mesmo que este não seja adequado com a presença de variáveis não estacionárias. Então, primeiro iremos encontrar a ordem $p$ do VAR, para então testar a presença de cointegração e, caso esta seja evidenciada, estimaremos um VEC com ordem $p-1$.
Para escolher a ordem $p$ do VAR, utilizaremos a função VARselect, que computa os critérios de informação do modelo para diferentes defasagens. Então, estimaremos o modelo com a função VAR e verificaremos se há ausência de correlação serial nos resíduos com a função serial.test (o lag escolhido para esse teste deve ser suficientemente grande para que a estatística do teste seja válida, para mais detalhes veja @lutkepohl2006). Depois, será conduzido o teste de coitegração de @johansen1991 com a função ca.jo e, caso seja verificada, estimaremos um VEC com ordem $p-1$ e o transformaremos em um VAR com uso da função vec2var, além de verificar a ausência de correlação serial nos resíduos. Por fim, estimaremos a Função de Resposta ao Impulso com relação a um choque na taxa Selic, utilizando a função irf, em que também adicionamos um intervalo de confiança de 95% obtido via bootstrap com 250 iterações.
Dado que iremos estimar sete modelos diferentes que possuem um passa-a-passo idêntico, demonstraremos o código para dois modelos, o geral e um específico, para que não fique muito repetitivo. Para estimar o restante, bastaria replicar o mesmo processo, apenas alterando a numeração dos objetos.
Modelo 1: Indústria Geral
# Renomeando a principal variável por simplicidade e mantendo apenas as variáveis relevantes para este modelo
db_industry_mod1 <- db_industry %>%
rename(Y_industry = `Indústria geral`) %>%
dplyr::select(Y_industry,
IPCA_M,
selic,
log_money_supply,
log_credito_sa,
log_cambio)
# Transformando em objeto Time Series
db_industry_mod1 <-
ts(db_industry_mod1,
start = c(2002, 1),
frequency = 12)
# Verificando a ordem do VAR com base nos Critérios de Informação
VARselect(
db_industry_mod1,
lag.max = 12,
type = 'both',
exogen = exogen,
season = 12 # dummies mensais
)
# Estimando o VAR
model1_var <- VAR(db_industry_mod1,
p = 2, # defasagem escolhida
type = 'both',
season = 12,
exogen = exogen)
# Teste de correlação serial
serial.test(model1_var, lags.pt = 30)
# Verificando a presença de cointegração
jotest <- ca.jo(
db_industry_mod1,
type = "trace",
K = 2, # defasagem escolhida para o VAR
ecdet = "trend", #
spec = "longrun",
dumvar = exogen,
season = 12
)
summary(jotest) # indica 4 relações de cointegração
# Transformando o VEC em VAR
model1 <- vec2var(jotest, r = 4) # r indica o número de relações de cointegração
# Teste de correlação serial
serial.test(model1, lags.pt = 30)
# Estimando a e plotando Função de Resposta ao Impulso
Y_IRF_mod1 <-
irf(
model1,
impulse = "selic",
response = "Y_industry",
n.ahead = 36,
boot = TRUE,
ci = 0.95,
runs = 250,
seed = 1414
)
g1 <- tibble(
IRF = Y_IRF_mod1$irf$selic,
Lower = Y_IRF_mod1$Lower$selic,
Upper = Y_IRF_mod1$Upper$selic
) %>%
ggplot(aes(x = seq(0, 36, 1))) +
geom_line(aes(y = IRF), size = 1.3, color = "#1874CD") +
geom_line(aes(y = Lower), color = 'red', linetype = "dashed") +
geom_line(aes(y = Upper), color = 'red', linetype = "dashed") +
geom_ribbon(aes(ymin = Lower, ymax = Upper),
alpha = 0.2,
fill = "#1874CD") +
geom_hline(aes(yintercept = 0), color = "black") +
labs(title = 'Produção Industrial Geral',
x = 'Meses após o choque',
y = '')
Modelo 2: Indústria Geral + Indústrias Extrativas
# Renomeando a principal variável por simplicidade e mantendo apenas as variáveis relevantes para este modelo
db_industry_mod2 <- db_industry %>%
rename(Y_industry = `Indústria geral`,
Y_industry_extrat = `Indústrias extrativas`) %>%
dplyr::select(Y_industry,
Y_industry_extrat,
IPCA_M,
selic,
log_money_supply,
log_credito_sa,
log_cambio)
# Transformando em objeto Time Series
db_industry_mod2 <-
ts(db_industry_mod2,
start = c(2002, 1),
frequency = 12)
# Verificando a ordem do VAR com base nos Critérios de Informação
VARselect(
db_industry_mod2,
lag.max = 12,
type = 'both',
exogen = exogen,
season = 12 # dummies mensais
)
# Estimando o VAR
model2_var <- VAR(db_industry_mod2,
p = 2, # defasagem escolhida
type = 'both',
season = 12,
exogen = exogen)
# Teste de correlação serial
serial.test(model2_var, lags.pt = 30)
# Verificando a presença de cointegração
jotest2 <- ca.jo(
db_industry_mod2,
type = "trace",
K = 2, # defasagem escolhida para o VAR
ecdet = "trend", #
spec = "longrun",
dumvar = exogen,
season = 12
)
summary(jotest2) # indica 5 relações de cointegração
# Transformando o VEC em VAR
model2 <- vec2var(jotest2, r = 5) # r indica o número de relações de cointegração
# Teste de correlação serial
serial.test(model2, lags.pt = 30)
# Estimando e plotando a Função de Resposta ao Impulso
Y_IRF_mod2 <-
irf(
model2,
impulse = "selic",
response = "Y_industry_extrat",
n.ahead = 36,
boot = TRUE,
ci = 0.95,
runs = 250,
seed = 1414
)
g2 <- tibble(
IRF = Y_IRF_mod2$irf$selic,
Lower = Y_IRF_mod2$Lower$selic,
Upper = Y_IRF_mod2$Upper$selic
) %>%
ggplot(aes(x = seq(0, 36, 1))) +
geom_line(aes(y = IRF), size = 1.3, color = "#1874CD") +
geom_line(aes(y = Lower), color = 'red', linetype = "dashed") +
geom_line(aes(y = Upper), color = 'red', linetype = "dashed") +
geom_ribbon(aes(ymin = Lower, ymax = Upper),
alpha = 0.2,
fill = "#1874CD") +
geom_hline(aes(yintercept = 0), color = "black") +
labs(title = 'Indústrias Extrativas',
x = 'Meses após o choque',
y = '')
Resultados
Fazendo o mesmo procedimento para o restante dos subsetores industriais, alterando apenas a numeração dos objetos em que armazenamos os resultados (e.g. no modelo geral era 1, no modelo que inclui indústrias extrativas é 2, e assim por diante), podemos juntar os gráficos em uma imagem.
layout_matrix <- matrix(c(1, 1, 1, 1,
2, 2, 3, 3,
4, 4, 5, 5,
6, 6, 7, 7), nrow = 4, byrow = TRUE)
grid <- grid.arrange(g1, g2, g3, g4, g5, g6, g7, layout_matrix = layout_matrix)
ggsave("Fig.png", grid, width = 7.7, height = 9.9, units = "in", dpi = 500)
Discussão sobre os resultados
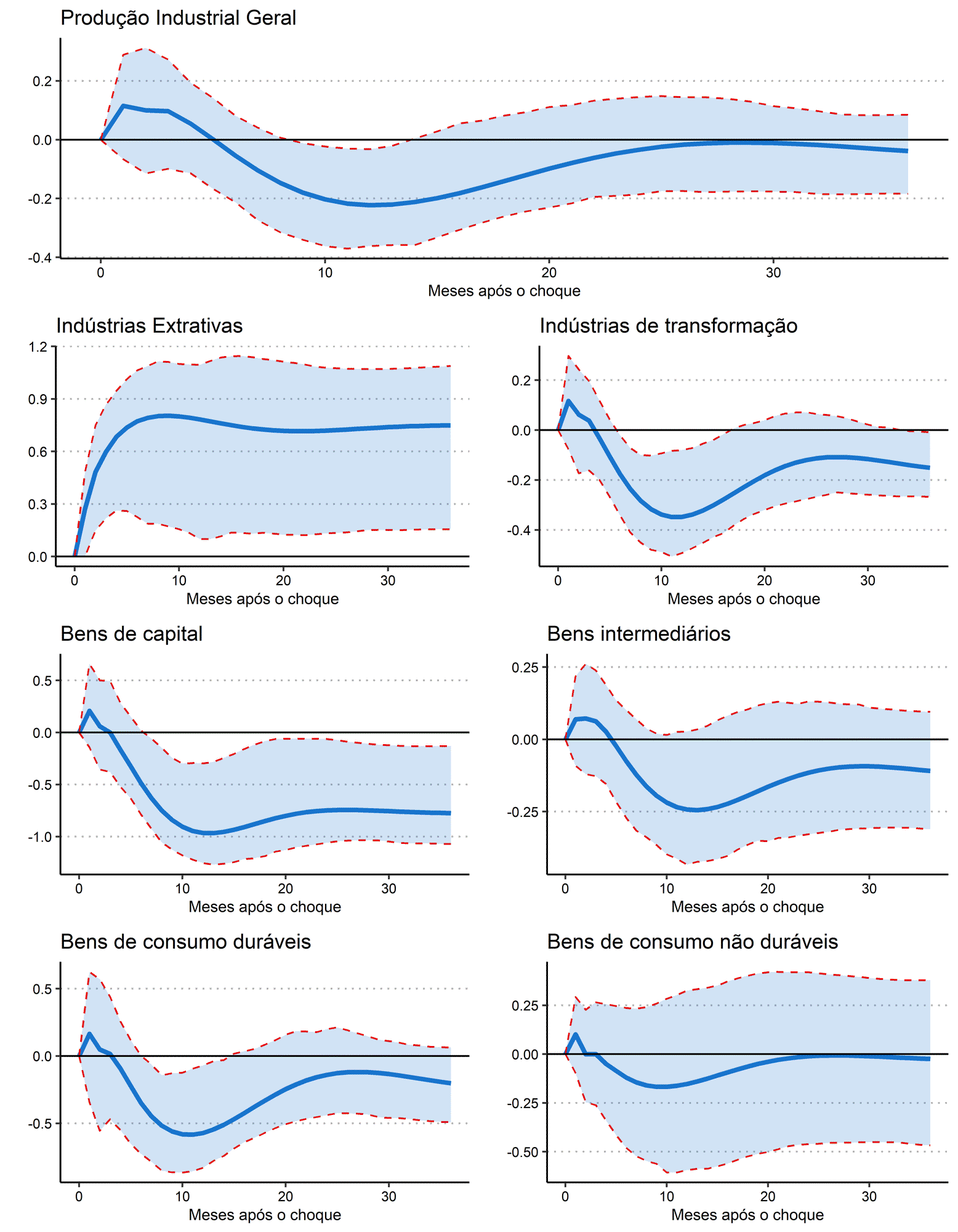
A Produção Industrial Geral apresenta uma reação levemente positiva nos primeiros meses após o choque, mas é rapidamente revertida e se torna declinante, chegando a um ponto de mínimo cerca de 12 meses após o aumento na taxa de juros. No entanto, o efeito é gradualmente dissipado e a produção industrial retorna para o nível anterior ao choque.
Ao analisar os subsetores industriais, pode-se observar uma disparidade em termos da direção da resposta e, principalmente, em termos de sua magnitude. O tempo entre o choque e o mês em que a resposta atinge um ponto de mínimo é similar entre os setores, indicando semelhanças originadas de uma rigidez contratual e produtiva.
O subsetor de Indústrias Extrativas é o único que apresenta uma resposta fortemente positiva e sustentada ao longo do tempo, em que a reação atinge um máximo cerca de dez meses após o choque e se mantém aproximadamente nesse nível até o final do período considerado. Por outro lado, o subsetor de Indústrias de Transformação apresenta uma leve resposta positiva nos primeiros meses, mas essa resposta é revertida e chega a um ponto de mínimo cerca de 12 meses após o choque na taxa de juros, com o impacto negativo sendo gradualmente exaurido ao longo dos próximos meses, mas permanecendo permanentemente menor do que o nível anterior à inovação de política monetária.
A resposta mais negativa pode ser observada no subsetor de Bens de Capital, sugerindo que o aumento no custo de capital da economia derivado do choque positivo na taxa de juros de curto prazo afeta permanentemente a produção de ativos de longo prazo, sendo o reflexo da redução nesse tipo de investimento por conta do maior custo de oportunidade. A Produção de Bens Intermediários apresenta uma reação positiva nos primeiros meses após o choque na taxa de juros, porém, essa situação é revertida e o subsetor passa a exibir uma resposta permanentemente negativa.
A produção de Bens de Consumo Duráveis é, assim como a produção de Bens de Capital, fortemente impactada pela inovação na taxa de juros, refletindo a sua grande dependência nas condições de financiamento da economia, por se tratar de bens com maior valor unitário. Assim, da mesma forma que empresas reduzem sua demanda por Bens de Capital por conta de uma deterioração das circunstâncias de financiamento, as famílias reduzem a sua demanda geral por Bens de Consumo Duráveis. Por outro lado, a produção geral de Bens de Consumo Não Duráveis é praticamente não afetada pelo choque na taxa de juros, mostrando uma relativa insensibilidade à política monetária, uma vez que considera bens mais relacionados ao consumo de subsistência dos agentes da economia.
References
Banco Central do Brasil. 2021a. “Ata Da Reunião 237 Do Comitê de Política Monetária.” Ata de reunião. Banco Central do Brasil. https://www.bcb.gov.br/publicacoes/atascopom/17032021.
—. 2021b. “Ata Da Reunião 238 Do Comitê de Política Monetária.” Ata de reunião. Banco Central do Brasil. https://www.bcb.gov.br/publicacoes/atascopom/05052021.
Bernanke, Ben S., and Alan S. Blinder. 1992. “The Federal Funds Rate and the Channels of Monetary Transmission.” The American Economic Review 82 (4): 901-21. http://www.jstor.org/stable/2117350.
Bernanke, Ben S., and Ilian Mihov. 1998. “Measuring Monetary Policy.” The Quarterly Journal of Economics 113 (3): 869-902. http://www.jstor.org/stable/2586876.
Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans. 1996. “The Effects of Monetary Policy Shocks: Evidence from the Flow of Funds.” The Review of Economics and Statistics 78 (1): 16-34. http://www.jstor.org/stable/2109845.
Dedola, Luca, and Francesco Lippi. 2005. “The Monetary Transmission Mechanism: Evidence from the Industries of Five OECD Countries.” European Economic Review 49 (6): 1543-69. https://doi.org/https://doi.org/10.1016/j.euroecorev.2003.11.006.
Dedola, Luca, and Francesco Lippi. 2005. “The Monetary Transmission Mechanism: Evidence from the Industries of Five OECD Countries.” European Economic Review 49 (6): 1543-69. https://doi.org/https://doi.org/10.1016/j.euroecorev.2003.11.006.
Dickey, David A., and Wayne A. Fuller. 1981. “Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root.” Econometrica 49 (4): 1057-72. http://www.jstor.org/stable/1912517.
Engle, Robert F., and C. W. J. Granger. 1987. “Co-Integration and Error Correction: Representation, Estimation, and Testing.” Econometrica 55 (2): 251-76. http://www.jstor.org/stable/1913236.
Johansen, Soren. 1991. “Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models.” Econometrica 59 (6): 1551-80. https://ideas.repec.org/a/ecm/emetrp/v59y1991i6p1551-80.html.
Lütkepohl, Helmut. 2006. New Introduction to Multiple Time Series Analysis. Springer Publishing Company, Incorporated.
Please, cite this work:
Kaebi, Mohammed (2022), “Funções de Resposta ao Impulso para a Produção Industrial com relação a choques na taxa Selic published at Open Code Community”, Mendeley Data, V1, doi: 10.17632/kr5gkryzyv.1