Estimadores da Volatilidade
Estimadores da Volatilidade
Para medir a volatilidade histórica, é comum calcular o desvio padrão dos retornos diários. No entanto, essa é uma medida que desconsidera as dinâmicas intraday. Imagine, por exemplo, uma ação que tenha fechamento do dia atual igual ao fechamento do dia anterior, mas que durante o dia oscilou 5%. Nessa situação, o indicador close-to-close não medirá a volatilidade com eficiência. Dessa forma, surgiram vários estimadores, cada um com seus pontos fortes e fracos, que auxiliam no cálculo da verdadeira volatilidade histórica. Alguns desses estimadores são:
- Close-to-Close (C): É a medida de volatilidade histórica mais comum, utiliza apenas dados de fechamento. Parkinson (HL) O primeiro estimador de volatilidade mais avançado surgiu em 1980, criado por Parkinson. Em vez de usar os preços de fechamento, utiliza as máximas e mínimas. Um ponto fraco do estimador é a premissa de mercados contínuos, o que leva a subestimar a volatilidade, pois movimentos como Gaps entre dias diferentes são ignorados.
- Garman-Klass (OHLC): Esse estimador é uma extensão de Parkinson, adicionando os preços de abertura e fechamento em seus cálculos. Como Gaps entre os dias são ignorados, também subestima a volatilidade.
- Garman-Klass-Yang-Zhang (OHLC): É uma extensão do estimador anterior, pois considera os saltos entre a abertura de um dia em relação ao fechamento do dia anterior.
- Rogers-Satchell (OHLC): O estimador de Rogers-Satchell foi criado no início da década de 90. É capaz de medir adequadamente a volatilidade com drift diferente de zero. No entanto, ainda não lida com saltos, subestimando a volatilidade.
- Yang-Zhang (OHLC): Em 2000, Yang-Zhang criaram o estimador mais poderoso, que lida tanto com Gaps de abertura quanto com drift diferente de zero. Seu cálculo envolve a soma da volatilidade do fechamento até a abertura do dia seguinte com a média ponderada do estimador de Rogers-Satchell e da volatilidade da abertura até o fechamento de um mesmo dia.
Nesse estudo, calculei a volatilidade em janelas móveis de 30 dias para o ibovespa desde junho/2014 até abril/2021. Importação do pacote do Yahoo e selecionando o código do Ibovespa:
from yahooquery import Ticker
ibov = Ticker("^bvsp")
Fazendo o upload das fórmulas dos estimadores:
from google.colab import files
uploaded = files.upload()
Saving estimadoresvol.jpg to estimadoresvol.jpg
Código para mostrar a imagem:
import cv2
from google.colab.patches import cv2_imshow
img = cv2.imread('estimadoresvol.jpg')
cv2_imshow(img)
cv2.waitKey()

Na Imagem, F é igual à frequência de retornos em um ano (252 para retornos diários, por exemplo).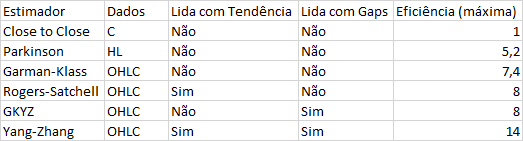
C - Dados de Fechamento H - Dados de Máxima L - Dados de Mínima O - Dados de Abertura Eficiência: Compara a variância de um estimador em relação à variância do estimador Close-to-Close. Mais detalhes podem ser encontrados no material: https://dynamiproject.files.wordpress.com/2016/01/measuring_historic_volatility.pdf Importando as cotações do Ibovespa de 01/06/2014 até 01/05/2021, com periodicidade diária. Observe que os dados são colocados em um dataframe.
df=ibov.history(start="2014-06-01",end="2021-05-01",interval='1d') type(df)
pandas.core.frame.DataFrame Número de linhas e colunas:
df.shape
(1707, 6)
Verificando se há valores nulos:
df.isnull().sum()
low 0
open 0
high 0
close 0
volume 0
adjclose 0
dtype: int64
df.dropna(inplace=True)
Primeiras linhas do DataFrame:
df.head()
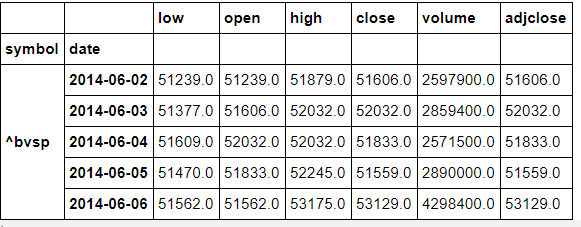
df=df[["open","low","high","close"]]
df
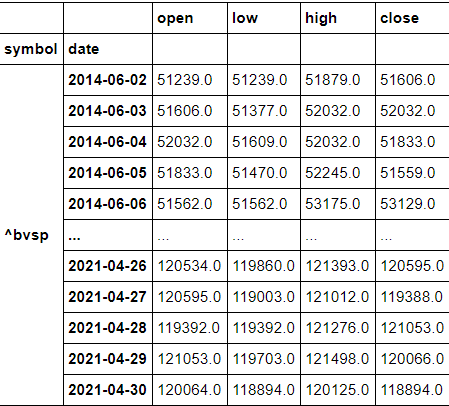
Nas funções abaixo, “df” é o dataframe com dados de abertura, mínima, máxima e fechamento e “n” é a janela móvel usada para o cálculo da volatilidade. O termo “np.sqrt(252)*100” anualiza os resultados. df[“close”] é a coluna do Dataframe com os dados de fechamento diário. df[‘high’] é a coluna do Dataframe com os dados de máxima diária. df[‘low’] é a coluna do Dataframe com os dados de mínima diária. df[‘open’] é a coluna do Dataframe com os dados de abertura diária.
def close_to_close(df,n):
df["C/C(-1)-1"]=df['close']/df['close'].shift(1)-1
df["Close-to-Close"]=df["C/C(-1)-1"].rolling(n).std()*np.sqrt(252)*100
return df["Close-to-Close"]
def Garman_Klass(df,n):
df["log^2(H/L)"]=(np.log(df['high']/df['low']))**2
df["log^2(C/O)"]=(np.log(df['close']/df['open']))**2
df["GK"]=0.5*df["log^2(H/L)"]-(2*np.log(2)-1)*df["log^2(C/O)"]
df["Garman-Klass"]=((df["GK"].rolling(n).mean())**0.5)*np.sqrt(252)*100
return df["Garman-Klass"]
def Parkinson(df,n):
df["log^2(H/L)"]=(np.log(df['high']/df['low']))**2
df["Parkinson"]=np.sqrt(df["log^2(H/L)"].rolling(n).mean()/4*np.log(2))*np.sqrt(252)*100
return df["Parkinson"]
def Yang_And_Zang(df,n):
df["o"]=np.log(df["open"]/df['close'].shift(1))
df["u"]=np.log(df["high"]/df["open"])
df["d"]=np.log(df["low"]/df["open"])
df["c"]=np.log(df["close"]/df["open"])
df["RS"]=np.log(df["high"]/df["close"])*np.log(df["high"]/df["open"])+np.log(df["low"]/df["close"])*np.log(df["low"]/df["open"])
k=0.34/(1.34+(n+1)/(n-1))
df["Yang And Zang"]=(((df["o"].rolling(20).std())**2+k*(df["c"].rolling(n).std())**2+(1-k)*df["RS"].rolling(n).mean())**0.5)*np.sqrt(252)*100
return df["Yang And Zang"]
def GKYZ(df,n):
df["o"]=np.log(df["open"]/df["close"].shift(1))
df["c"]=np.log(df["close"]/df["open"])
df["log^2(H/L)"]=(np.log(df['high']/df['low']))**2
df["GKYZ"]=np.sqrt(((df["o"]**2)+0.5*df["log^2(H/L)"]-(2*np.log(2)-1)*(df["c"]**2)).rolling(n).mean())*np.sqrt(252)*100
return df["GKYZ"]
Concatenando o resultado das funções, todas com n=30 dias, em um DataFrame e retornando o valor da última linha
df1=pd.concat([close_to_close(df,30),Parkinson(df,30),Garman_Klass(df,30),Rogers_Satchell(df,30),GKYZ(df,30),Yang_And_Zang(df,30)],axis=1)
df1[-1:]

df1.dropna(inplace=True)
df1
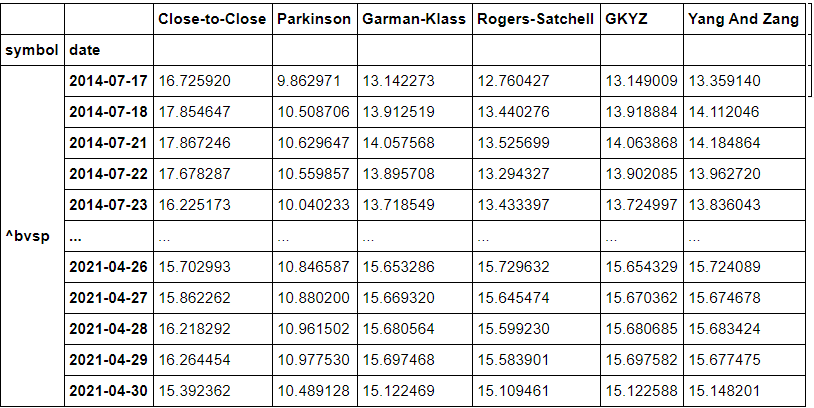
Plotando os estimadores separadamente para o período selecionado:
df1.plot(subplots=True, figsize=(20,12)); plt.legend(loc='best')
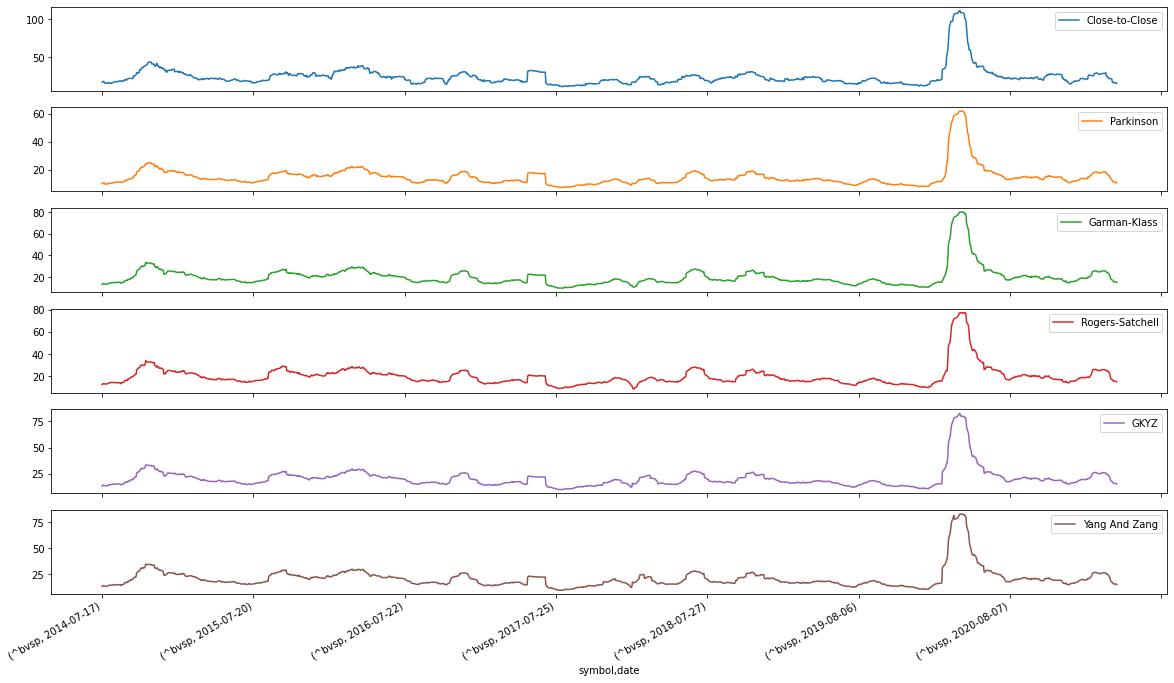
Plotando os estimadores em um mesmo gráfico para o período selecionado:
df1.plot(subplots=False, figsize=(20,8)); plt.legend(loc='best')
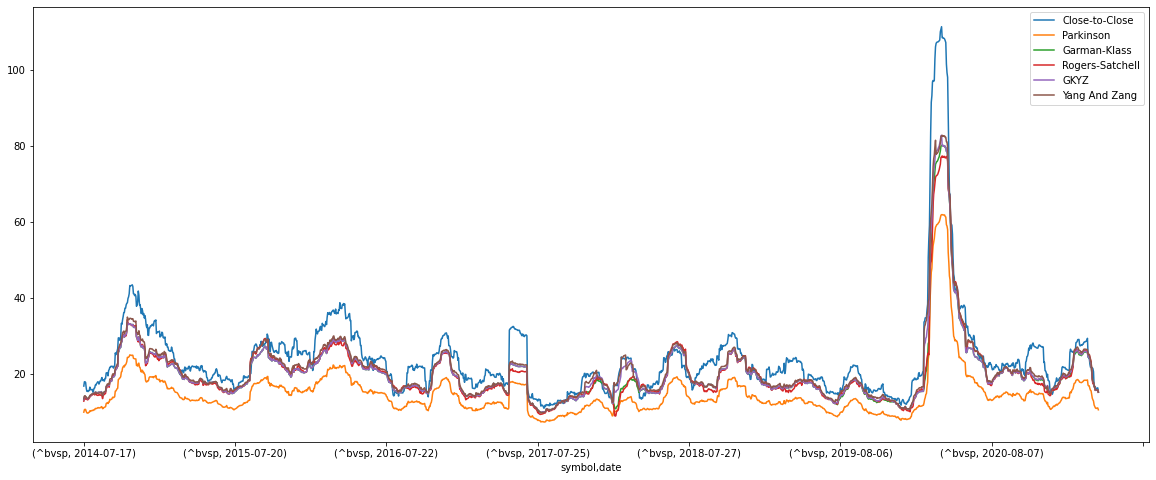
Please, cite this work:
Mendes, Bernardo (2022), “Estimadores de Volatilidade published at Open Code Community”, Mendeley Data, V1, doi: 10.17632/n9b8sp6xwf.1