Modelagem de Volatilidade via GARCH Models
Modelagem de Volatilidade via GARCH Models published at the "Open Code Community"
Definida como qualquer medida de variabilidade (eg. variância, desvio-padrão), volatilidade tem um papel fundamental na determinação das decisões de investimento dos participantes do mercado, sobretudo para aqueles interessados em problemas de gestão de portfolio e gerenciamento de risco.
Embora seja um componente extremamente importante no campo de finanças, volatilidade é uma variável latente, sendo necessária a sua estimação de forma a se obter uma medida razoável para se fazer inferência. Diversas especificações paramétricas foram propostas para modelagem da volatilidade da série de retornos de ativos nas últimas décadas. Entre elas, uma abordagem bastante popular e com grande impacto na literatura de finanças são os modelos da família ARCH, capitaneados por Engle (1982) e Bollerslev (1986). Tais modelos consideram a variância condicional como a defasagem distribuída do quadrado dos retornos passados de um ativo subjacente, isto é
$$
\begin{equation}
\begin{array}{l}
r_{t}=a_{t}=\sigma_{t} \varepsilon_{t}\
E\left(r_{t}^{2} \mid \mathbf{I}_{t-1}\right)=\sigma_{t}^{2}=\omega+\sum_{i=1}^{m} \alpha_{i} a_{t-i}^{2}
\end{array}
\end{equation}
$$
onde $r_{t}$ são os retornos indexados em $t=1, \ldots, T $, $\sigma_{t}$ é o componente de volatilidadee $\varepsilon_{t}$ são os choques, que tipicamente assumem normalidade $\varepsilon_{t} \ticksim N(0,1)$.
Em nosso exercício, vamos apresentar uma forma fácil para estimar diversas especificações dessa natureza. Para tanto, vamos usar uma estratégia semelhante ao artigo, estimando, para cada ticker, quarenta especificações derivadas da combinação de cinco modelos dessa classe, mais a modelagem de $\varepsilon_{t}$ considerando oito distribuições distintas.Pegando carona com meu xará Victor Gomes, vou utilizar os mesmos ativos mencionados no post. Vamos considerar uma amostra que considera um período superior a sete anos, o que deve ser suficiente para se ter uma boa ideia de como a volatilidade se comporta para ativos do mercado de ações brasileiro.
library(BatchGetSymbols)
library(rugarch)
library(tidyverse)
tickers = c('EQTL3.SA', 'PETR4.SA', 'VALE3.SA', 'WEGE3.SA','EMBR3.SA',
'CSNA3.SA', 'USIM5.SA','TOTS3.SA','ABEV3.SA','LREN3.SA','CIEL3.SA',
'RADL3.SA', 'RENT3.SA', 'MDIA3.SA','EZTC3.SA', 'FLRY3.SA','OIBR3.SA','CVCB3.SA')
assets <- BatchGetSymbols(tickers,
first.date = '2014-01-01',
last.date = Sys.time(),
type.return = "log",
freq.data = "daily")
assets <- assets[[2]]
daily_returns <- assets %>%
select(c(ref.date,ticker,ret.closing.prices)) %>%
pivot_wider(id_cols = ref.date,names_from = ticker,values_from = ret.closing.prices)
De acordo com algumas surveys, é bem documentado na literatura de finanças empíricas que a taxa de retorno de séries financeiras exibem certos atributos como caudas pesadas, agrupamento de volatilidade e efeito de alavancagem. Tomemos como exemplo o ticker PETR4.SA, conforme mostra as figuras abaixo:
plot.returns <- ggplot(daily_returns) +
geom_line(aes(x = ref.date, y = PETR4.SA)) +
labs( x = "Date" , y = 'Returns') +
theme_light() +
ggtitle('PETR4.SA') +
theme(text = element_text(size=12),
plot.title = element_text(size=12),
panel.grid.minor = element_blank(),
panel.grid.major = element_blank())
plot.volatility <- ggplot(daily_returns) +
geom_line(aes(x = ref.date, y = abs(PETR4.SA))) +
labs( x = "Date" , y = 'Absolute returns') +
theme_light() +
ggtitle('PETR4.SA') +
theme(text = element_text(size=12),
plot.title = element_text(size=12),
panel.grid.minor = element_blank(),
panel.grid.major = element_blank())
qqplot <- ggplot(daily_returns, aes(sample = PETR4.SA)) +
stat_qq() +
stat_qq_line() +
labs(x = 'Theoretical' ,y = 'Sample') +
ggtitle('QQ plot: ') +
theme_light() +
theme(text = element_text(size=12),
plot.title = element_text(size=12),
panel.grid.minor = element_blank(),
panel.grid.major = element_blank())
histogram <- ggplot(daily_returns) +
geom_histogram(aes(x=PETR4.SA,y = ..density..),
color="white", fill="Dark grey",linetype="solid",alpha = 0.8) +
geom_density(aes(x = PETR4.SA,y = ..density..),color="black") +
labs(x = '',y = 'Density') +
ggtitle('Histogram') +
theme_light() +
theme(text = element_text(size=12),
plot.title = element_text(size=12),
panel.grid.minor = element_blank(),
panel.grid.major = element_blank())
cowplot::plot_grid(plot.returns,qqplot,plot.volatility,histogram, nrow = 2)

Em particular, a clusterização da volatilidade implica presença de elevada autocorrelação no quadrado dos retornos:
list.acf <- acf(na.omit(daily_returns$PETR4.SA^2),
lag.max = 50, type = "correlation", plot = FALSE)
N <- as.numeric(list.acf$n.used)
df1 <- data.frame(lag = list.acf$lag, acf = list.acf$acf)
df1$lag.acf <- dplyr::lag(df1$acf, default = 0)
df1$lag.acf[2] <- 0
df1$lag.acf.cumsum <- cumsum((df1$lag.acf)^2)
df1$acfstd <- sqrt(1/N * (1 + 2 * df1$lag.acf.cumsum))
df1$acfstd[1] <- 0
ci = 0.95
ggplot(data = df1, aes(x = lag, y = acf)) +
geom_area(aes(x = lag, y = qnorm((1+ci)/2)*acfstd), fill = "darkgray", alpha = 0.4) +
geom_area(aes(x = lag, y = -qnorm((1+ci)/2)*acfstd), fill = "darkgray", alpha = 0.4) +
geom_col(fill = "black", width = 0.2) +
scale_x_continuous(breaks = seq(0,max(df1$lag),6)) +
scale_y_continuous(name = element_blank(),
limits = c(-.1,1)) +
theme_light() +
ggtitle('ACF of squared returns') +
theme(text = element_text(size=12),
plot.title = element_text(size=12),
panel.grid.minor = element_blank(),
panel.grid.major = element_blank())
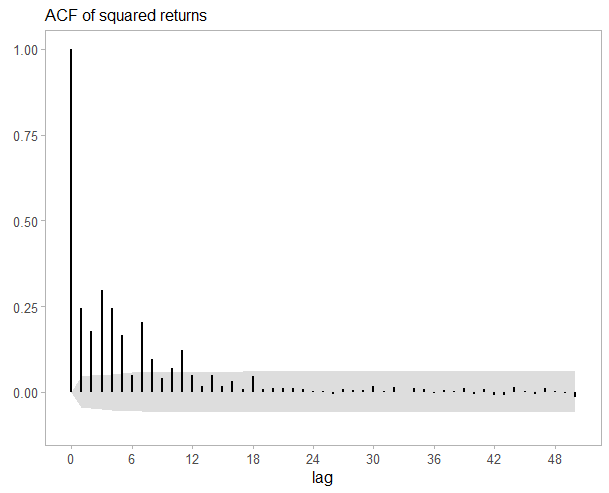
A autocorrelação presente no quadrado dos retornos de séries financeiras sugere que a variância condicional dos retornos apresente uma dependência temporal dos choques passados. Diante desses fatos, é preciso que se faça a modelagem da variância utilizando especificações adequadas que capturam os fatos estilizados das séries de retorno, tais como os modelos de heterocedasticidade condicional do tipo GARCH.
Para estimar os modelos da família ARCH, vamos considerar diversas especificações com a ordem do GARCH (1,1), uma vez que é bem documentado na literatura que dificilmente uma especificação com ordem diferente deverá ser mais eficiente do que esta. Nosso objetivo difere do paper mencionado, pois este tem foco na previsão, enquanto nosso interesse reside em apenas fazer a seleção de modelos baseando-se no critério de informação de Schwarz, embora o package rugarch ofereça outros três critérios distintos. Observe, no decorrer do código, que estabelecemos um critério de seleção automática das especificações para cada ticker.
date <- daily_returns %>%
select(ref.date) %>%
rename(date = ref.date) %>%
slice(-1)
daily_returns <- daily_returns %>%
select(-ref.date) %>%
slice(-1)
garch.models <- c("sGARCH","eGARCH","gjrGARCH","apARCH","csGARCH")
distributions <- c("norm","snorm","std","sstd","ged","sged","jsu","ghyp")
specification <- list()
for(i in 1:length(garch.models)){
for(j in 1:length(distributions)){
specification[[paste(garch.models[i],distributions[j],sep = "-" )]] <-
ugarchspec(variance.model = list(model = garch.models[i], garchOrder = c(1,1)),
mean.model = list(armaOrder = c(0, 0)),
distribution.model = distributions[j])
}
}
specifications <- names(specification)
IC = output = volatility = fit.garch = sigma = info.criteria <- list()
progress_bar <- winProgressBar(title="Progress Bar",
label="0% done", min=0, max=100, initial=0)
for(t in 1:ncol(daily_returns)){
returns <- as.matrix(daily_returns[,t])
for(s in 1:length(specifications)){
fit.garch[[s]] <- ugarchfit(spec = specification[[s]],
solver = 'hybrid', data = returns)
sigma[[s]] <- sigma(fit.garch[[s]])
info.criteria[[s]] <- cbind.data.frame(tickers[t],
rownames(infocriteria(fit.garch[[s]])),
specifications[s],
infocriteria(fit.garch[[s]]))
}
info_criteria <- bind_rows(info.criteria[1:length(specifications)]) %>%
rename(c(Ticker = `tickers[t]`,IC = `rownames(infocriteria(fit.garch[[s]]))`,
Specification = `specifications[s]`,Statistic = V1)) %>%
pivot_wider(id_cols = c(Specification,IC), names_from = Ticker, values_from = Statistic) %>%
filter(IC == 'Bayes') %>%
arrange(.[[3]]) %>%
slice(1)
IC[[t]] <- info_criteria
names(fit.garch) = names(sigma) <- specifications
model.select <- as.character(info_criteria[1,1])
output[[t]] <- fit.garch[[model.select]]
volatility[[t]] <- sigma[[model.select]]
info <- sprintf("%d%% done", round((t/ncol(daily_returns))*100))
setWinProgressBar(progress_bar, t/ncol(daily_returns)*100, label=info)
}
close(progress_bar)
De acordo com nosso critério de seleção de modelos, a combinação do GARCH padrão mais a modelagem do choque pela distribuição t-student é mais recorrente, sendo escolhida sete vezes em 18 ativos considerados.
| Specification | Ticker | BIC |
|---|---|---|
| apARCH-std | CIEL3.SA | -4.711838 |
| apARCH-std | CVCB3.SA | -4.541972 |
| eGARCH-jsu | USIM5.SA | -3.895312 |
| eGARCH-std | PETR4.SA | -4.261241 |
| eGARCH-std | EMBR3.SA | -4.837635 |
| eGARCH-std | ABEV3.SA | -5.564423 |
| gjrGARCH-std | EQTL3.SA | -5.437899 |
| gjrGARCH-std | LREN3.SA | -4.910334 |
| gjrGARCH-std | RADL3.SA | -5.055834 |
| gjrGARCH-std | RENT3.SA | -4.736320 |
| sGARCH-jsu | OIBR3.SA | -3.585446 |
| sGARCH-std | VALE3.SA | -4.468457 |
| sGARCH-std | WEGE3.SA | -5.126926 |
| sGARCH-std | CSNA3.SA | -3.801952 |
| sGARCH-std | TOTS3.SA | -4.865413 |
| sGARCH-std | MDIA3.SA | -5.053061 |
| sGARCH-std | EZTC3.SA | -4.588863 |
| sGARCH-std | FLRY3.SA | -5.069654 |
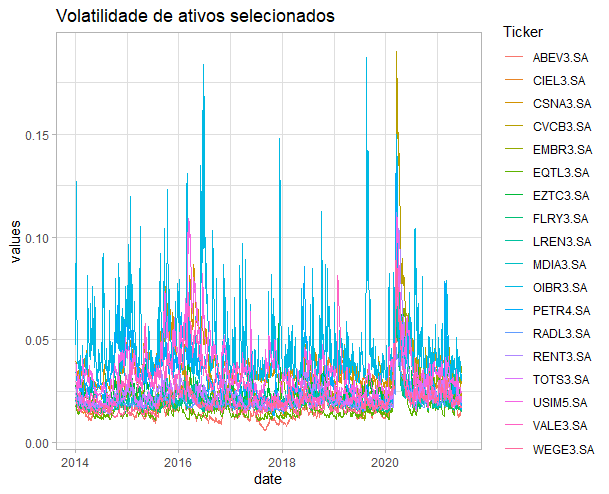
Por último, vamos plotar todas as séries de volatilidade dos retornos estimadas em um só gráfico para avaliar a evolução deste componente ao longo do tempo. Embora alguns papéis sejam mais voláteis em determinados instantes de tempo, observe que a volatilidade durante o momento mais agudo da crise do Covid-19, em meados de fevereiro de 2020, foi muito mais acentuada e com impacto bastante uniforme sobre todos os ativos selecionados.
ts.volatility <-cbind.data.frame(date,
as.matrix(bind_cols(volatility[1:length(daily_returns)])))
names(ts.volatility) <- c('date',tickers)
ts.volatility %>%
pivot_longer(cols = EQTL3.SA:CVCB3.SA, names_to = "Ticker", values_to = "values") %>%
arrange(Ticker,date) %>%
ggplot() +
geom_line(aes(x = date, y = values, color = Ticker)) +
theme_light() +
ggtitle('Volatilidade de ativos selecionados')
theme(legend.position = 'right',
plot.title = element_text(size=12),
panel.grid.minor = element_blank(),
panel.grid.major = element_blank())
Conforme discutido anteriormente, a volatilidade dos retornos de séries financeiras exibe um certo grau de previsibilidade. Portanto, deixo para o leitor o desafio de como realizar previsão com modelos do tipo GARCH, de tal forma a também contribuir conosco nesse projeto.
Please, cite this work:
Henriques, Victor (2021), “Modelagem de Volatilidade via GARCH Models published at the “Open Code Community””, Mendeley Data, V1, doi: 10.17632/s3nzk8zwk7.1