Detecting time series outliers

A função tsoutliers () do pacote forecasting do R é útil para identificar anomalias em uma série temporal. No entanto, não está devidamente documentado em nenhum lugar. Esta postagem visa preencher essa lacuna.

A função começou como uma resposta em CrossValidated e depois foi adicionada ao pacote forecasting, dado que achei que poderia ser útil para outras pessoas. Desde então, ele foi atualizado e tornou-se mais confiável.

O procedimento decompõe a série temporal em tendência, sazonalidade e componentes remanescentes:

$$y_t = T_t + S_t + R_t$$

O componente sazonal é opcional e pode conter vários padrões sazonais correspondentes aos períodos sazonais dos dados. A ideia é remover qualquer sazonalidade e tendência nos dados e, em seguida, descobrir os outliers nas séries restantes, $R_t$.

Para dados observados com mais frequência do que anualmente, usamos uma abordagem robusta para estimar $T_t$ e $S_t$ aplicando primeiro o método MSTL aos dados. O MSTL estimará iterativamente o (s) componente (s) sazonal (is).

Em seguida, a força da sazonalidade é medida usando:

$$F_s = 1 - \dfrac{Var(y_t-\hat{T}_t-\hat{S}_t)}{Var(y_t -\hat{T}_t)}$$

Se $F_s$ > 0,6, uma série ajustada sazonalmente é calculada:

$$y^*_t = y_t - \hat{S}_t$$

Um limite de força sazonal é usado aqui porque a estimativa de S_t provavelmente será super ajustada e muito barulhenta se a sazonalidade subjacente for muito fraca (ou inexistente), potencialmente mascarando quaisquer outliers por tê-los absorvidos no componente sazonal.

Se $Fs$< 0,6, ou se os dados são observados anualmente ou com menos frequência, simplesmente definimos $y_t^* = y_t$.

Em seguida, nós reestimamos o componente de tendência a partir dos valores de y_t. Para séries temporais não sazonais, como dados anuais, isso é necessário, pois não temos a estimativa de tendência da decomposição STL. Mas mesmo que tenhamos calculado uma decomposição STL, podemos não tê-la usado se $F_s$< 0,6.

O componente de tendência T_t é estimado aplicando o o Friedman’s super smoother (via supsmu()) aos dados $y_t^*$. Esta função foi testada em muitos dados e tende a funcionar bem em uma ampla gama de problemas.

Procuramos outliers na série restante estimada:

$$\hat{R}_t = y_t^* - \hat{T}_t$$

Se Q1 denota o 25º percentil e Q3 denota o 75º percentil dos valores restantes, então o intervalo interquartil é definido como IQR = Q3 - Q1. As observações são rotuladas como outliers se forem menores que Q1-3 × IQR ou maiores que Q3 + 3 × IQR. Esta é a definição usada por Tukey (1977, p44) em sua proposta original de boxplot para valores “distantes”.

Se os valores restantes são normalmente distribuídos, então a probabilidade de uma observação ser identificada como um outlier é de aproximadamente 1 em 427000.

Quaisquer outliers identificados desta maneira são substituídos por valores interpolados linearmente usando as observações vizinhas, e o processo é repetido.

Exemplo: dados de ouro

Os dados do preço do ouro contêm os preços diários do ouro pela manhã em dólares americanos de 1 ° de janeiro de 1985 a 31 de março de 1989. Os dados me foram fornecidos por um cliente que queria que eu fizesse uma previsão do preço do ouro. (Eu disse a ele que seria quase impossível superar uma previsão ingênua). Os dados são mostrados a seguir.

library(fpp2)
autoplot(gold)

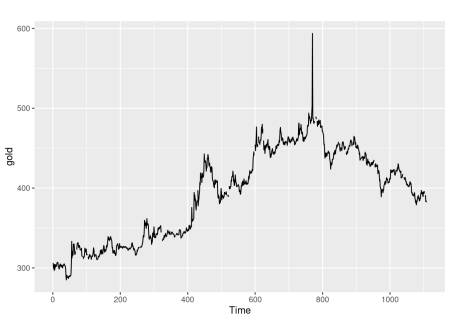
Existem períodos de valores ausentes e um outlier óbvio que é cerca de $ 100 maior do que o esperado. Isso foi simplesmente um erro de digitação, com alguém digitando 593,70 em vez de 493,70. Vamos ver se a função tsoutliers () pode identificá-lo.

tsoutliers(gold)
## $index
## [1] 770
## 
## $replacements
## [1] 495

Com certeza, ele é facilmente encontrado e a substituição sugerida (interpolada linearmente) está perto do valor verdadeiro.

A função tsclean () remove outliers identificados dessa maneira e os substitui (e quaisquer valores ausentes) por substituições interpoladas linearmente.

autoplot(tsclean(gold), series="clean", color='red', lwd=0.9) +
autolayer(gold, series="original", color='gray', lwd=1) +
geom_point(data = tsoutliers(gold) %>% as.data.frame(), 
aes(x=index, y=replacements), col='blue') +
labs(x = "Day", y = "Gold price ($US)")

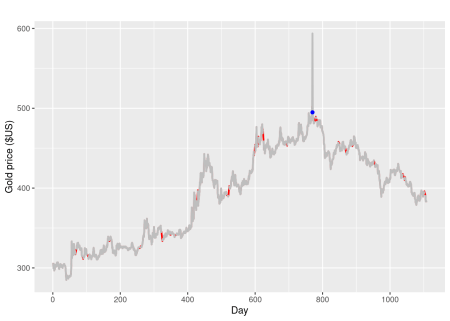
O ponto azul mostra a substituição do outlier, as linhas vermelhas mostram a substituição dos valores ausentes.

O post em inglês se encontra no link: https://robjhyndman.com/hyndsight/tsoutliers/