Regresão linear simples usando R

Introdução

Esse post visa elucidar como podemos fazer uma regressão linear simples no R, utilizando uma base de dados disponibilizada no Livro de Wooldridge. Vamos explorar um exemplo contido no seu capítulo 2.

O que é uma regressão linear simples?

A regressão linear simples é uma maneira de relacionar duas variáveis de maneira linear, ou seja, através desse grupo de dados, traçar uma reta que minimiza o erro ao quadrado entre a nuvem de pontos de um gráfico y-x e uma reta a ser estimada. É uma ferramenta poderosa para predição e para analisar a tendência e relacionamento entre variáveis.

A reta em questão é usada para relacionar as variáveis $x$ e $y$ da seguinte forma:

$$y = β_0 + β_1x + u$$

Uma vez que é uma regressão linear simples, essa equação conta com apenas duas variáveis $x$ e $y$ sendo $y$ a variável dependente e $x$ a variável independente. Nessa equação, os elementos que ainda não são conhecidos são $β_0$, $β_1$ e $u$.

$β_0$ e $β_1$ são conhecidos como betas e são os valores a serem estimados. $β_1$ é onde tipicamente recai nosso interesse.

Base de dados

A base de dados utilizada é a base ceosal1 do livro do Wooldridge, que contém dados de salários de CEOs e roe das suas respectivas empresas. Nesse caso, vamos identificar a relação entre roe e salário, em que salário será a variável dependente e roe a variável independente.

    data(ceosal1, package = 'wooldridge')
    
    # Para anexar o dataframe e conseguir usar suas variáveis sem precisar chamar o dataframe.
    attach(ceosal1)
    
    #Para vizualizar os primeiros itens da base de dados.
    head(ceosal1)

Podemos estimar a reta de duas maneiras diferentes, conforme a seguir.

Cálculo manual dos betas

A primeira é calculando os betas manualmente através das fórmulas abaixo:

$$ \hat{β}_0 = \overline{y} -\hat{β}_1\overline{x} $$

$$ \hat{β}_1= \frac{Cov(x,y)}{Var(x)} $$

O código para calcular usando o R:

    # Visualizando os valores que vão compor as equações.
    mean(salary)
    mean(roe)
    var(roe)
    cov(roe, salary)
    
    # Cálculo de β1. Como queremos visualizar o valor, colocamos entre parenteses.
    (b1 <- cov(roe, salary)/var(roe))
    
    # Cálculo de β0
    (b0 <- mean(salary) - b1*mean(roe))

Apesar de permitir entender mais explicitamente como esses coeficientes são calculados, essa maneira é um pouco mais trabalhosa. Alternativamente, existe uma forma mais eficiente.

Calculando o beta automaticamente com a função do R

  # A variavel RLS vai conter o modelo linear
  RLS <- lm(salary ~ roe)

Obs.: Como foi usada a função $attach()$ no começo do código não foi preciso especificar a base de dados.

Visualizando a reta

Por fim, podemos plotar o gráfico do roe pelo salary e visualizar a reta de regressão.

  # Como os dados possuem alguns outliers usamos o ylim pra delimitar o limite do gráfico no eixo y
  plot(roe, salary, ylim=c(0,5000))
 
  # Para adicionar a linha de tendência
  abline(RLS)

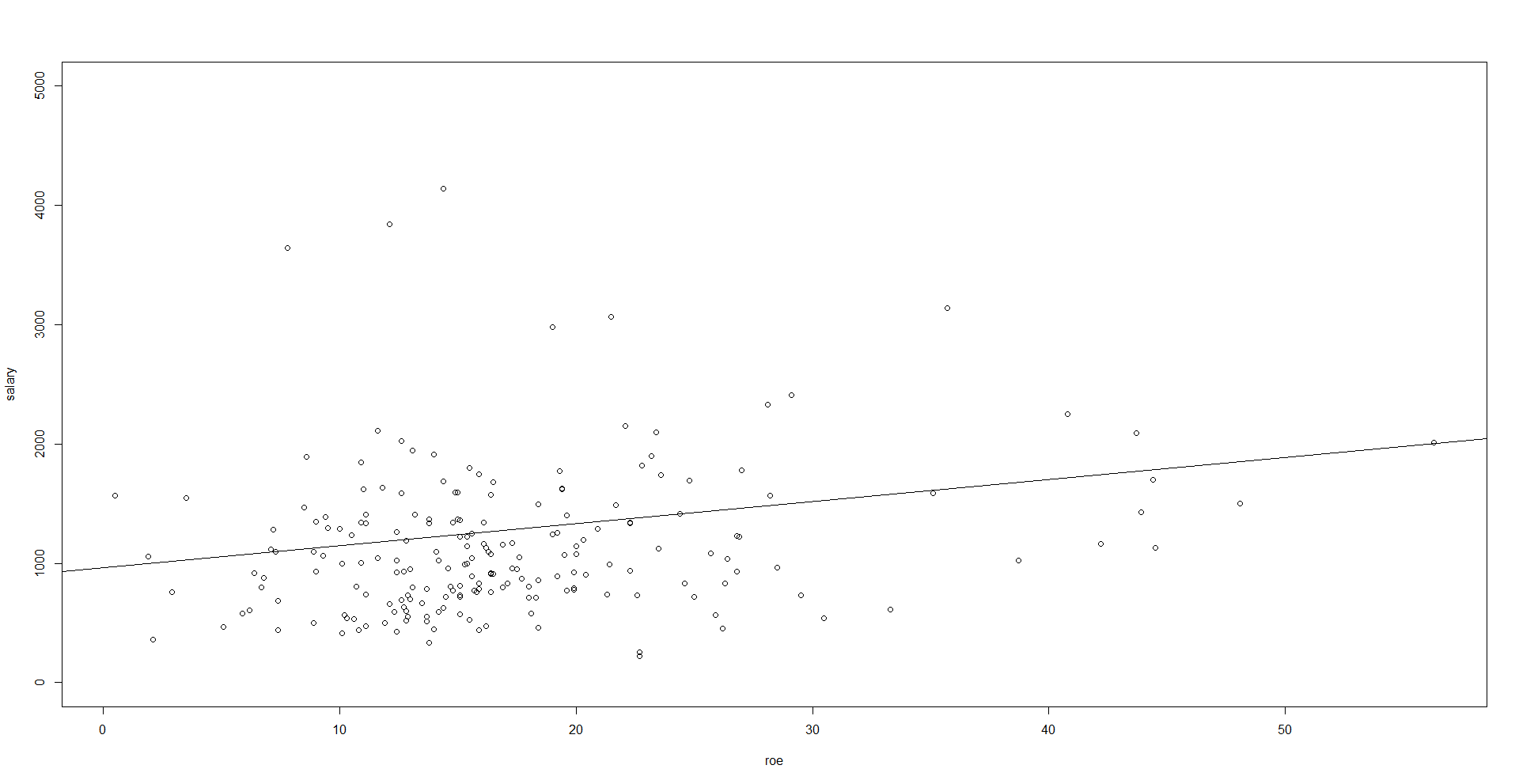
Após visualizar o gráfico, fica muito mais fácil entender o que a regressão linear simples faz. Além disso, o gráfico mostra como a reta fica o mais próximo possível da maior quantidade de pontos plotados. Isto é, como a reta estimada é aquela que minimiza a distância (ao quadrado) entre a reta e os pontos.