Propriedades de um modelo de regressão linear no R

Introdução

O post de hoje continuará apresentando conceitos básicos de regressão linear simples. Vamos seguir com exemplos do cap. 2 do livro do Wooldridge.

Exemplo de predição e visualização do erro

Seguindo a linha da primeira publicação, continuaremos usando os dados de retorno sobre patrimônio líquido e os salários de CEOs da base ceosal1 do Wooldridge.

Seguindo o exemplo 2.6 do livro, calcularemos o erro de cada observação e observaremos que esse erro varia individualmente entre as diferentes observações de $x$.

#base de dados
data(ceosal1, package='wooldridge')

#fixar a base de dados
attach(ceosal1)

salario <- salary

roe <- roe

#regressão linear
rl <- lm(salario ~ roe)

salario_prev <- fitted(rl)

u_prev <- resid(rl)

cbind(roe, salario, salario_prev, u_prev)[1:10,]

Essa tabela nos ajuda a perceber que, para cada par $x-y$ de observação, temos um valor de erro específico $u_{prev}$. Também para cada valor de $x$, temos um valor projetado para $y$, isto é, $salario_{prev}$.

Validando duas propriedades de um modelo de regressão linear

Vamos falar agora um pouco sobre duas propriedades de um modelo de regressão linear.

Propriedade 1

A média dos resíduos é $0$. Em outras palavras, os coeficientes Beta são escolhidos de forma a tornar a soma dos residuos igual a zero.

$$\sum_{i=1}^n\hat{u}_i=0$$

Propriedade 2

Além disso, caso pluguemos o valor médio de $x$, i.e., $\bar{x}$, no modelo de regressão, vamos achar o valor médio de $y$, i.e., $\bar{y}$.

$$\bar{y} = \hat\beta_0+\hat\beta_1.\bar{x}$$

Demostração das propriedades

Abaixo, demonstramos essas duas propriedades.

data(wage1, package='wooldridge')

#fixar a base de dados
attach(wage1)

#regressão linear
rl <- lm(wage ~ educ)

beta_prev <- coef(rl)

salario_prev <- fitted(rl)

u_prev <- resid(rl)

#propriedade 1
mean(u_prev)

#propriedade 2
mean(wage)

beta_prev[1] + beta_prev[2] * mean(educ)

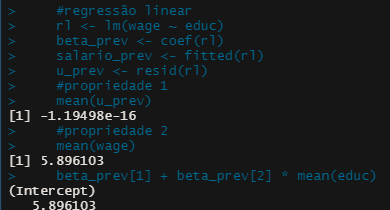
Esperamos que esse material introdutório seja útil!