Precificação de títulos de dívida no R

Introdução

Em muitos setores, o preço de um ativo não reflete exatamente o seu valor, nos mercados de capitais tal como nos mercados de crédito esse conceito de valor diferente do preço é comum.

Quando falamos sobre Bonds esse conceito também está presente, o valor de uma Bond para um credor pode ser diferente e, geralmente, vai ser diferente do preço que ele paga para comprar aquele título de dívida.

Nesses casos o conceito de valor está intrinsecamente ligado a possibilidade de aquele ativo gerar receitas no futuro trazidas a valor presente.

Nesse artigo, Vamos mostrar como se calcular o preço de um título de dívida, sua duration e sua duration modificada. Além disso, vamos criar uma calculadora (i.e., uma função) para cálculo do preço do título.

Exemplo de valor do dinheiro

Supondo que uma pessoa compre um título por 1000 reais e ele renda 15% ao ano, no entanto o dinheiro desvalorize a uma taxa de 10% ao ano:

#valor atual
pv <- 1000

#taxa (lembrar que no R a virgula é o ponto)
r <- 0.15

#valor futuro 1, para dois anos, usando a fórmula de juros compostos
(fv1 <- (pv *(1+r)^1))

#valor futuro 2, para um ano
(fv2 <- (pv*(1+r)^2))

Fica claro que o tempo é uma variável importante na equação.

#taxa de desvalorização do dinheiro
i <- 0.10

#valor presente 1 dos recebimentos
(pv1 <- (fv1/(1+i)^1))

#valor presente 2
(pv2 <- (fv2/(1+i)^2))

Apesar de, em ambos os casos, os recebimentos no futuro serem maior quando trazidos a valor presente, eles justamente são menores quando trazidos a valor presente.

Por isso é importante entender que quando for comparar rendimentos eles devem estar em uma base de tempo igual.

Data frame de fluxos de caixa

Vamos criar agora um data frame para facilitar a execução da análise acima.

Alguns dos termos utilizados nesse tópico são em inglês, conforme a seguir:

• Face value (valor de face) é o valor que será recebido ao vencimento do título
• Coupon (cupom) é uma porcentagem do valor que é paga antecipadamente ao valor de face, por exemplo se a bond tem 5% de cupom por mês significa que ela pagará, além do valor de face no seu vencimento, um montante de 5% do valor de face durante todos os meses até o vencimento.
• Maturity (vencimento) é o tempo que demora para a bond pagar seu face value.

Exemplo

Suponha que exista um bond com valor de face de 1000, coupon de 10% e a maturity 5 anos, vamos fazer seus fluxos de caixa de recebimento:

#fluxo de caixa
fc <- c(100, 100, 100, 100, 1100)

fc <- data.frame(fc)

#adicionando a coluna dos anos
fc$ano <- as.numeric(c(1, 2, 3, 4, 5))

#vendo o data frame
view(fc)

Trazendo os fluxos de caixa a valor presente

Sendo a taxa de desconto 5%.

#taxa de desconto
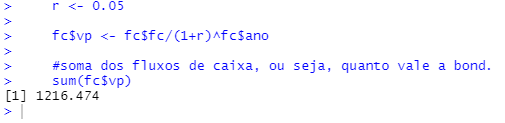
r <- 0.05

fc$vp <- fc$fc/(1+r)^fc$ano  

#soma dos fluxos de caixa, ou seja, quanto vale 0 bond.
sum(fc$vp)

Automatizando o valuation da Bond

Podemos criar uma função para apenas adicionar os parâmetros e calcular quanto o bond vale com base em seus fluxos de caixa.

# FV -> face value
# C -> coupon
# T -> tempo
# Y -> a taxa de desconto esperada
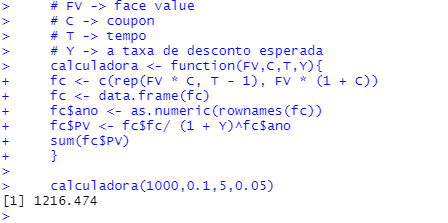
calculadora <- function(FV,C,T,Y){
fc <- c(rep(FV * C, T - 1), FV * (1 + C))
fc <- data.frame(fc)
fc$ano <- as.numeric(rownames(fc))
fc$PV <- fc$fc/ (1 + Y)^fc$ano
sum(fc$PV)
}

calculadora(1000,0.1,5,0.05)

Exemplo de precificação de Bonds com diferentes riscos atrelados

Primeiro vamos pegar o yield de um bond classificado com rating AAA e outro com rating BAA para comparar.

# instalando a biblioteca (só precisa rodar uma vez)
install.packages ("Quandl")

# chamando a biblioteca
library(Quandl)

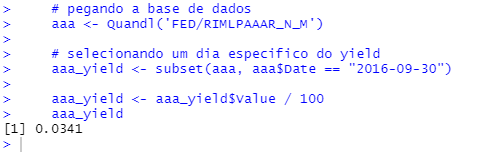
# pegando a base de dados
aaa <- Quandl('FED/RIMLPAAAR_N_M')

# selecionando um dia especifico do yield
aaa_yield <- subset(aaa, aaa$Date == "2016-09-30")

aaa_yield <- aaa_yield$Value / 100
aaa_yield

# pegando a base de dados
baa <- Quandl('FED/RIMLPBAAR_N_M')

# selecionando um dia especifico do yield
baa_yield <- subset(baa, baa$Date == "2016-09-30")

baa_yield <- baa_yield$Value / 100
baa_yield

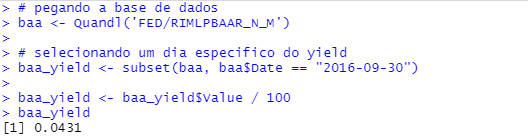
Como demonstrado um título BAA tem um yield maior já que a ele possui um risco menor.

Mas como esse yield impacta o valor justo da bond?

Calculando o valor dos bonds

Os valores escolhidos para o bond são 1000 de face value, 10% de coupon e 5 anos de maturidade.

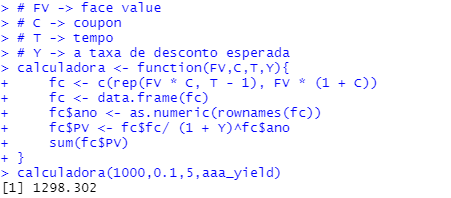
Calculando valor da bond classificada como AAA:

calculadora(1000,0.1,5,aaa_yield)

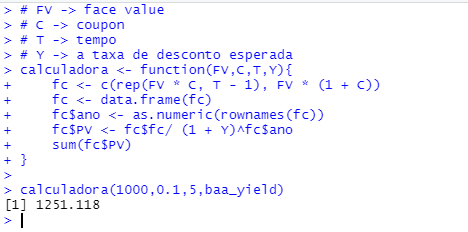
Calculando valor da bond classificada como BAA:

calculadora(1000,0.1,5,baa_yield)

Entendendo melhor o comportamento do preço em relação ao yield

A seguir, para entender o comportamento do preço com uma variação no yield plotaremos um gráfico.

#criando um data frame com diferentes yields
yields <- seq(0.05,0.5, 0.01)

yields <- data.frame(yields)

#calculando o preço das bonds 1
for (i in 1:nrow(yields)){
yields$preço1[i] <- calculadora(1000,0.1,5,yields$yields[i])
}

#calculando o preço das bonds 2
for (i in 1:nrow(yields)){
yields$preço2[i] <- calculadora(1000,0.1,20,yields$yields[i])
}

#plotando grafico
library(hrbrthemes)
library(ggplot2)

ggplot(data=yields, aes(x=yields)) + geom_line(aes(y=preço1, colour='red')) + geom_line(aes(y=preço2, colour='blue')) + geom_point(aes(y=preço1, colour='red')) + geom_point(aes(y=preço2, colour='blue')) + theme_modern_rc() + labs(x='Yields',
y='Valor',title = 'Titulos com diferentes maturidades')

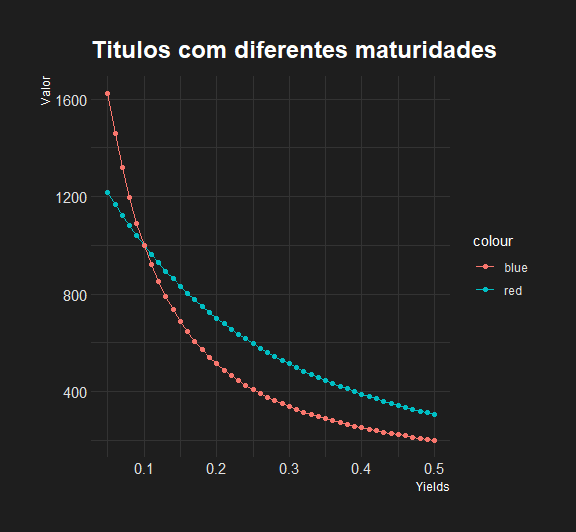
O título representado pela linha vermelha possi 5 anos de maturidade e o representado pela linha azul possui 20.

Podemos notar que o preço dos títulos se comportam de forma diferente para variações na taxa de juros.

Usando yields mais atuais dos bonds

O código a seguir mostra como conseguir uma base de dados mais atual dos yields.

install.packages(treasuryTR)

library(treasuryTR)

#pegando a base de dados de yields de 5 anos.
yield_5y <- get_yields("DGS5")

#buscando uma data atual
(data <- Sys.Date())
if (weekdays(data) == "domingo" ){
data <- data - 9
} else if (weekdays(data) == "sábado" ){
data <- data - 8
} else {
data <- data - 7
}

yield <- as.numeric(yield_5y$DGS5[data])

calculadora(1000,0.0,5,yield)

Calculando o preço com relação ao yield atual

library(treasuryTR)

#pegando a base de dados de yields de 5 anos.
yield_5y <- data.frame(yield = as.numeric(get_yields("DGS5")))

#usando uma bond com maturity 5 anos, Face value 1000 e cupom 0%.
for (i in 1:nrow(yield_5y)){
yield_5y$preço[i] <- calculadora(1000,0.0,5,yield_5y$yield[i])
}

#plotando grafico
plot(yield_5y, type='l', color='red', main='preço x yield')

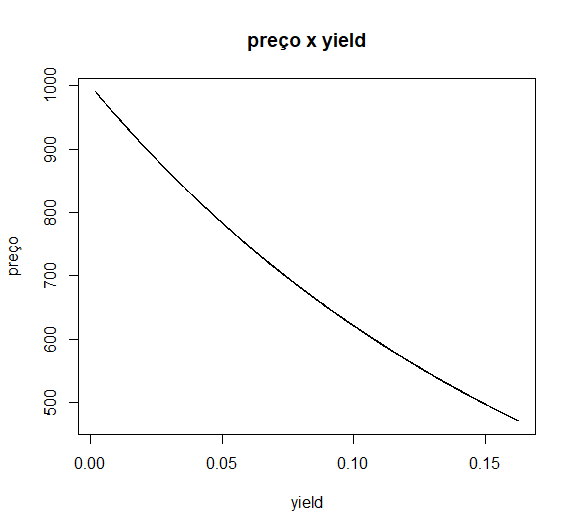
Duration

Por fim, iremos entender a duration, que nada mais é do que uma medida do tempo médio para receber os fluxos de caixa do título.

Esse conceito será importante se o bond paga cupons, pois esses pagamentos fazem que o bond tenha duration diferente de sua maturidade, i.e., na média, os fluxos de caixa recebidos ocorrerão antes da maturidade.

A fórmula da duration:

$$ Duration = \frac{1PV(C_1)}{PV}+\frac{2PV(C_2)}{PV}+…+\frac{nPV(C_n)}{PV} $$

Sendo:

• $PV(c_1)$ o valor presente do cupom 1
• $PV(c_2)$ o valor presente do cupom 2
• $PV$ o valor presente do bond

Calculando a duration

Usando os mesmos dados para calcular a duration.

library(treasuryTR)

yield_5y <- get_yields("DGS5")

#buscando uma data atual
(data <- Sys.Date())
if (weekdays(data) == "domingo" ){
data <- data - 9
} else if (weekdays(data) == "sábado" ){
data <- data - 8
} else {
data <- data - 7
}

yield <- as.numeric(yield_5y$DGS5[data])

# FV -> face value
# C -> coupon
# T -> tempo
# Y -> a taxa de desconto esperada
duration <- function(FV,C,T,Y){
fc <- c(rep(FV * C, T - 1), FV * (1 + C))
fc <- data.frame(fc)
fc$ano <- as.numeric(rownames(fc))
fc$PV <- fc$fc/ (1 + Y)^fc$ano
pv <- sum(fc$PV)
fc$dur <- fc$ano*fc$PV/pv
sum(fc$dur)
}

duration(1000,0.1,5,yield)

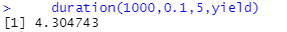
Modified duration

O último tópico abordado será a modified duration que representa uma medida da mudança do valor de um título relacionado a mudança no yield.

Ou seja, a modified duration representa uma mensuração de quanto seria a mudança percentual do preço do bond caso o yield alterasse em $1$% para mais ou para menos.

$$ MD = \frac{Duration}{(1+YTM)} $$

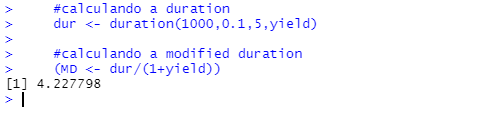
#calculando a duration
dur <- duration(1000,0.1,5,yield)

#calculando a modified duration
(MD <- dur/(1+yield))

Esperamos que tenha gostado desse material! Obrigado pela leitura!