Carteira de opções

Ações possuem uma exposição direta tanto ao risco idiossincrático quanto ao risco sistemático.

Segundo Salles et al (2009) risco total na teoria de finanças, ou simplesmente o risco ou a volatilidade, de ativos, ou mercados, tem dois componentes: o risco sistemático, ou risco de mercado, e o risco específico, ou risco idiossincrático. Enquanto o risco de mercado, denominado também risco não diversificável, é a parcela que não se elimina em portfólios eficientemente diversificados, a parcela que se refere ao risco específico de ativos, ou de mercados, pode ser minimizada, ou até eliminada, com a diversificação eficiente de um portfólio.

As opções, por outro lado, têm exposição não só ao ativo subjacente, mas também às taxas de juros, tempo e volatilidade. Essas exposições são entradas para o modelo de preços de opções Black-Scholes. Uma vez que esses insumos afetam o valor da opção em questão, o derivativo parcial da função pode nos dizer como o valor da opção muda quando uma dessas exposições muda segurando as outras constantes.

As gregas

Usando uma expansão da série Taylor, podemos derivar todas as gregas. As gregas nos dizem como podemos esperar que uma opção ou portfólio de opções mude quando uma mudança ocorre em uma ou mais das exposições de opções. Algo importante a notar é que todas as aproximações de primeira ordem são lineares, e a função de preços de opção não é linear. Isso significa que quanto mais o parâmetro subjacente se desviar do cálculo inicial de derivativo parcial, menos preciso será. É por isso que as gregas são atualizados, geralmente, em tempo real, para que possamos constantemente ter um novo conjunto de expectativas para opção ou valor de portfólio quando algo muda.

Dynamic Hedging

Vamos considerar o seguinte caso:

Imagine que você tenha uma posição short em 10.000 calls de PETRE316, e queremos proteger essa exposição a mudanças de volatilidade, movimentos no ativo subjacente e a velocidade de movimentos no ativo subjacente. Você, menino(a) esperto(a) que é, quer fazer um gerenciamento de risco para construir um hedge dinâmico para ser reequilibrado diariamente. Como podemos neutralizar a exposição dela à vega, delta e gama da opção?

A primeira coisa a perceber é que para neutralizar a exposição às gregas vamos precisar de posições compensadas em outras opções. Há três gregas para neutralizar, por isso precisamos de três opções para criar três equações de gregas e pesos com três incógnitas (os pesos nas outras opções negociáveis). No entanto, o truque aqui é perceber que a derivada parcial do ativo subjacente em relação a si mesma é apenas 1, isso significa que o ativo subjacente tem um delta de 1 e todos os outros valores de gregas são 0. Isso significa que podemos construir um portfólio de duas opções negociáveis, encontrar pesos apropriados para neutralizar as gregas, em seguida, tomar uma posição de compensação no ativo subjacente — efetivamente neutralizando a exposição às três gregos.

Vamos ao racional da estrutura

Inicialmente precisamos de 2 libs:

• options (lib forked por mim e modificada)
• bizdays (instalar via pip)

from options import blackscholes as bs #hashABCD/opstrat
from bizdays.bizdays import Calendar #pip3 install https://github.com/wilsonfreitas/python-bizdays

cal = Calendar.load(filename=r"C:\Users\maike\anaconda3\Lib\bizdays\ANBIMA.cal")


asset_price = 33.85
strike_price = 31.01
time_to_expiration = cal.bizdays('2022-04-12', '2022-05-20')
risk_free_rate = 11.75
qtd = 10000


bsm = {'short_petr4': bs.black_scholes(K=33.76,
                                        St=asset_price,
                                        r=risk_free_rate,
                                        t=time_to_expiration,
                                        v=31.30,
                                        type='c')}
bsm['short_petr4']['greeks']
bsm['short_petr4']['value']

{‘option value’:1.610085917163115,
‘intrinsic value’: 0.09000000000000341,
‘time value’: 1.5200859171631116}
{‘delta’: 0.5782157973095728,
‘gamma’: 0.11496483723977133,
‘theta’: -0.033981308417225554,
‘vega’: 0.0425401992365655,
‘rho’: 0.018532757514520395}
Para as condições acima consideramos:
* Short 10.000 PETR4 Call@31,01
* Vol implicita 31,31%
* 26 DU para vencimento
* RiskFree 11,75%

Usando essas entradas, podemos encontrar o valor teórico da posição da opção em R$1,610086

Isso significa que teremos um prêmio de R$16.100,86 pela venda das opções.

E as gregas?

Vamos considerar mais duas calls, com strike em R$34,51 (PETRE341) e R$35,26 (PETRE338)

bsm['a'] = bs.black_scholes(K=34.51,
                        St=asset_price,
                        r=risk_free_rate,
                        t=time_to_expiration,
                        v=32.95,
                        type='c')

bsm['b'] = bs.black_scholes(K=35.26,
                        St=asset_price,
                        r=risk_free_rate,
                        t=time_to_expiration,
                        v=33.66,
                        type='c')

STRIKE: R$33,76
{‘short_petr4’: {‘value’: {‘option value’: 1.610085917163115, ‘intrinsic value’: 0.09000000000000341, ‘time value’: 1.5200859171631116},
‘greeks’: {‘delta’: 0.5782157973095728, ‘gamma’: 0.11496483723977133, ‘theta’: -0.033981308417225554, ‘vega’: 0.0425401992365655, ‘rho’: 0.018532757514520395}},
STRIKE: R$34,51
‘a’: {‘value’: {‘option value’: 1.31496432880253, ‘intrinsic value’: 0, ‘time value’: 1.31496432880253},
‘greeks’: {‘delta’: 0.4940209712555761, ‘gamma’: 0.11134245473105785, ‘theta’: -0.03466675982936925, ‘vega’: 0.04337169189784432, ‘rho’: 0.01589677715290344}},
STRIKE: R$35,26
‘b’: {‘value’: {‘option value’: 1.0397762028222335, ‘intrinsic value’: 0, ‘time value’: 1.0397762028222335},
‘greeks’: {‘delta’: 0.4163378582310132, ‘gamma’: 0.10660029457749903, ‘theta’: -0.03354462845811788, ‘vega’: 0.04241921913964324, ‘rho’: 0.013467649514116532}}}

Usando uma combinação desses ativos podemos neutralizar a exposição do nosso portfólio à delta, gama e vega. A questão é como? A resposta: álgebra linear.

Neutralizando as gregas

As gregas que estamos interessados em neutralizar no portfólio atual podem ser expressos como um vetor…

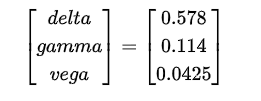
O objetivo é encontrar os pesos dos três ativos que somos capazes de negociar para neutralizar esses valores. Primeiro, vamos procurar neutralizar gama e vega, em seguida, usando o ativo subjacente, vamos neutralizar delta …

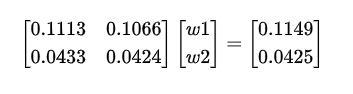
Isso significa inverter a matriz contendo os valores das gregas para as opções negociáveis podemos encontrar os pesos apropriados…

Podemos fazer isso usando Python…

import numpy as np

greeks = np.array([[bsm['a']['greeks']['gamma'], bsm['b']['greeks']['gamma']], [bsm['a']['greeks']['vega'], bsm['b']['greeks']['vega']]])
portfolio_greeks = [[bsm['short_petr4']['greeks']['gamma']*qtd], [bsm['short_petr4']['greeks']['vega']*qtd]]

# We need to round otherwise we can end up with a non-invertible matrix
inv = np.linalg.inv(greeks)
print(inv)

[[ 425.78952313 -1070.01707043]
[ -435.35011688 1117.61724204]]

Nós efetivamente encontramos o inverso da matriz, o produto ponto será os pesos resultantes para ambas as opções negociáveis…

w = np.dot(inv, portfolio_greeks)
print(w)

[[ 34320.83862493]
[-25062.95183441]]

print(np.round(np.dot(greeks, w) - portfolio_greeks))

[[0.]
[0.]]

Agora que a exposição a gama e vega é neutralizada, precisamos neutralizar nossa nova exposição ao Delta. Para encontrar nossa nova exposição, pegamos a soma-produto de todas as posições de opção em nosso portfólio com seus respectivos deltas…

# Greeks including delta
portfolio_greeks = [[bsm['short_petr4']['greeks']['delta']*-qtd],
                    [bsm['short_petr4']['greeks']['gamma']*-qtd],
                    [bsm['short_petr4']['greeks']['vega']*-qtd]]

greeks = np.array([[bsm['a']['greeks']['delta'], bsm['b']['greeks']['delta']],
                    [bsm['a']['greeks']['gamma'], bsm['b']['greeks']['gamma']],
                    [bsm['a']['greeks']['vega'], bsm['b']['greeks']['vega']]])

print(np.round(np.dot(greeks, w) + portfolio_greeks))

[[738.]
[ 0.]
[ 0.]]

Depois de multiplicar nossas novas posições de opções pelas gregas originais, descobrimos que nossa posição líquida delta é 738. Isso significa que, ao vender ações do ativo subjacente (PETR4), teremos um portfólio neutro delta, gama e vega. Isso significa que o valor da nossa carteira de opções não mudará quando houver mudanças no preço do ativo subjacente, na volatilidade dos ativos subjacentes ou na velocidade em que o preço do ativo subjacente muda. Portfólio Neutro Delta, Gama e Vega -10.000 calls PETRE316 34.321 calls PETRE341 -25.063 calls PETRE338 -738 PETR4

REFERÊNCIAS

enegep2009_TN_STO_104_693_13487.pdf (abepro.org.br) Algorithmic Portfolio Hedging. Python and Black-Scholes Pricing for… | by Roman Paolucci | Towards Data Science