Grafos e modelo de blocos aninhados para matrizes de correlação: clusterização do mercado de ações
Esse post é da série sobre filtragem em grafos (esparsificação). O post anterior pode ser acessado em: Grafos e filtragem de arestas: conceitos e confusões.
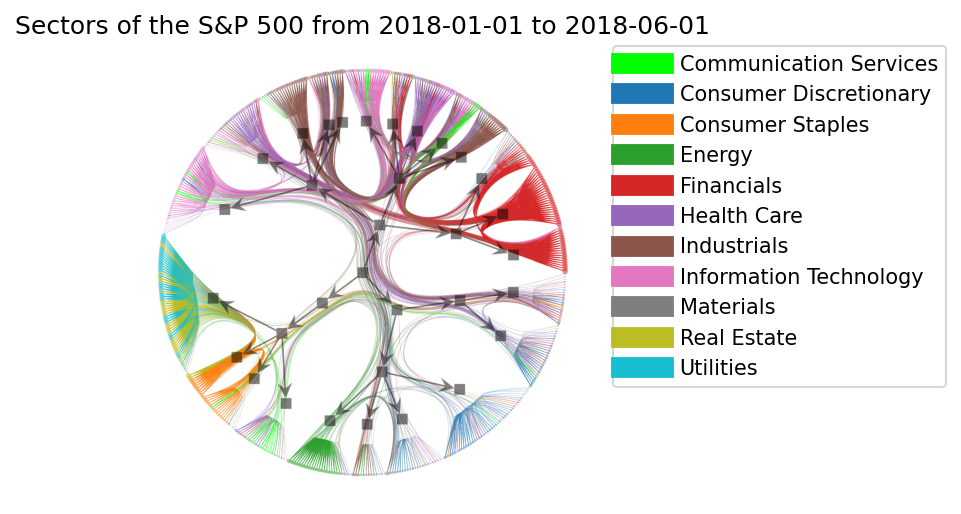
O objetivo é mostrar como usar o modelo de bloco estocástico aninhado (nSBM) para o processo de análise exploratória do mercado de ações. O nSBM e SBM são modelos não-paramétricos estabelecidos numa sólida base estatística. Vou te ensinar na prática como usar eles no python e como analisar os outputs, que a primeira vista podem parecer artísticos ou complexos. Veja só:
A ordem que seguiremos nesse post é:
- Uma introdução meio longa para te situar em grafos e o porquê usar eles aqui.
- Código
- Construção da matriz de correlação entre os retornos dos ativos
- Filtragem da matriz de correlação via um filtro de grafos
- Inferência e visualização do nSBM
- Como analisar o nSBM?
- Extra: MST
Para reproduzir esse post recomendo usar um ambiente conda, pois uma das bibliotecas depende de diversas coisas além de libs usais do python
Comece checando se você tem as seguintes bibliotecas instaladas
matplotlib, pandas, yfinance
Instale o igraph com
$ pip install python-igraph
O graph-tool, do excelente Tiago Peixoto via conda-forge
$ conda install -c conda-forge graph-tool
Não menos importante, você precisa instalar minha biblioteca de filtragem de grafos, o edgeseraser deixe seu star aqui :).
$ pip install edgeseraser
Introdução
Análise exploratória é usada tanto como o objetivo final em si como uma ferramenta que fornece subsídios para melhores tomadas de decisões para escolha de modelos preditivos ou pré-seleção de instâncias para serem analisadas com mais detalhes.
Contudo, muitas das técnicas exploradas e ensinadas na web se restringem àquelas que podem ser empregadas quando o conjunto de dados vive em algum espaço organizado (como o $\mathbb R^n$) e cujos dados não têm relação entre si. Um conjunto de pontos. Mas e os dados que não se enquadram nisso?
Um exemplo de conjunto de dados extremamente complicado são as redes sociais. Redes sociais são conjuntos de pessoas e a existência de pelo menos relações pares a pares (hyper-grafos é um assunto para outro post) podendo ser negativas, positivas ou algo mais complicado. Cada pessoa em uma rede social pode ser identificada por um conjunto de features tais como gostos pessoais, horário de uso do sistema, etc. Representar uma rede social por pontinhos é reducionista. É para isso que grafos podem ser empregados
Grafos
Um grafo armazena objetos que têm relações pares a pares entre si. Sendo possível associar a cada objeto ou relação um outro tipo de dado genérico tais como um número real, um vetor ou mesmo outro grafo. Mas é importante ressaltar que grafos estão em todo lugar, por exemplo em matrizes de correlação. Portanto, usar grafos para analisar correlações é válido, especialmente quando muitas dessas correlações podem ou queremos que sejam descartadas.
Matrizes de correlação
No OpenCode matrizes de correlação já apareceram em diversos posts:
Mas o que é uma matriz de correlação se não um conjunto de relações pares a pares com valores reais? Bom, então a questão aqui fica evidente: Uma matriz de correlação pode ser analisada usando ferramentas feitas para analisar grafos! Ok, isso pode ser feito, mas você pode se perguntar o porquê de fazer isso.
Uma atividade muito comum quando exploramos matrizes de correlação é tentar encontrar grupos de elementos fortemente/fracamente correlacionados, isso não é uma tarefa trivial à medida que o número de elementos aumenta. Além disso, é comum jogarmos fora as relações que são muito fracas. Quando fazemos isso estamos esparsificando a matriz, na terminologia de grafos estamos filtrando arestas! No post anterior eu discuti o porquê disso poder ser bem perigoso..
Uma maneira mais elaborada de se analisar matrizes de correlação é através da construção de árvores de expansão mínima (MST), apesar do nome complicado é um processo bem simples de construir um grafo e você pode encontrar diversos tutoriais sobre MST e o mercado de ações na internet.
Devido a tutoriais com MST estarem já espalhados, decidi fazer algo diferente aqui e propor usar um método pouco conhecido para exploração de grafos e aplicar ele em matrizes de correlação de ativos. Esse método é conhecido pela sigla nSBM, modelo de bloco estocástico aninhado (nested Stochastic Block Model) e é um método não-paramétrico para inferência de comunidades em grafos que permite analisar a hierarquia de comunidades.
Uma das grandes qualidades dos SBM e variantes é que eles são construídos em cima de um arcabouço estatístico rigoroso e ao mesmo tempo é possível detectar comunidades com pouquíssimos vértices. Isso é ótimo, pois duas coisas que não queremos é que o método que escolhamos diga que certas coisas formam comunidades mesmo que não passe de um amontoado de coisas aleatórias e que ele bote coisas onde não devia só porque são pequenas demais, isso é uma crítica aos métodos de detecção por maximização de modularidade
Baixando e criando nosso grafo
Extraindo o preço de fechamento
Vamos começar importando o que for necessário
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import igraph as ig
from edgeseraser.disparity import filter_ig_graph
mpl.rcParams.update(_VSCode_defaultMatplotlib_Params)
plt.style.context('classic')
mpl.rcParams['figure.facecolor'] = 'white'
Usaremos uma tabela contendo os simbolos de um conjunto de ativos e os setores. O csv tem a seguinte organização, e está disponível aqui.
| Symbol | Name | Sector |
|---|---|---|
| MMM | 3M | Industrials |
| AOS | A. O. Smith | Industrials |
| ABT | Abbott Laboratories | Health Care |
| ABBV | AbbVie | Health Care |
!wget https://raw.githubusercontent.com/datasets/s-and-p-500-companies/master/data/constituents.csv
df = pd.read_csv("constituents.csv")
all_symbols = df['Symbol'].values
all_sectors = df['Sector'].values
all_names = df['Name'].values
# Criaremos um dicionário para mapear um simbolo para seu
# setor e uma cor
symbol2sector = dict(zip(all_symbols, all_sectors))
symbol2name = dict(zip(all_symbols, all_names))
Hora de baixar as informações sobre os ativos. Iremos computar as correlações numa janela de um semestre.
start_date = '2018-01-01'
end_date = '2018-06-01'
try:
prices = pd.read_csv(
f"sp500_prices_{start_date}_{end_date}.csv", index_col="Date")
tickers_available = prices.columns.values
except FileNotFoundError:
df = yf.download(
list(all_symbols),
start=start_date,
end=end_date,
interval="1d",
group_by='ticker',
progress=True
)
tickers_available = list(
set([ticket for ticket, _ in df.columns.T.to_numpy()]))
prices = pd.DataFrame.from_dict(
{
ticker: df[ticker]["Adj Close"].to_numpy()
for ticker in tickers_available
}
)
prices.index = df.index
prices = prices.iloc[:-1]
del df
prices.to_csv(
f"sp500_prices_{start_date}_{end_date}.csv")
Retorno e matrizes de correlação
A correlação será calculada para todos os ativos considerando o retorno. O retorno que estamos calculando aqui é simplesmente a mudança percentual do preço de fechamento do ativo.
returns_all = prices.pct_change()
# a primeira linha não faz sentido, não existe retorno no primeiro dia
returns_all = returns_all.iloc[1:, :]
returns_all.dropna(axis=1, thresh=len(returns_all.index)//2., inplace=True)
returns_all.dropna(axis=0, inplace=True)
symbols = returns_all.columns.values
Para calcular a correlação é fácil
# plot the correlation matrix with ticks at each item
correlation_matrix = returns_all.corr()
plt.title(f"Correlation matrix from {start_date} to {end_date}")
plt.imshow(correlation_matrix)
plt.colorbar()
plt.savefig("correlation.png", dpi=150)
plt.clf()
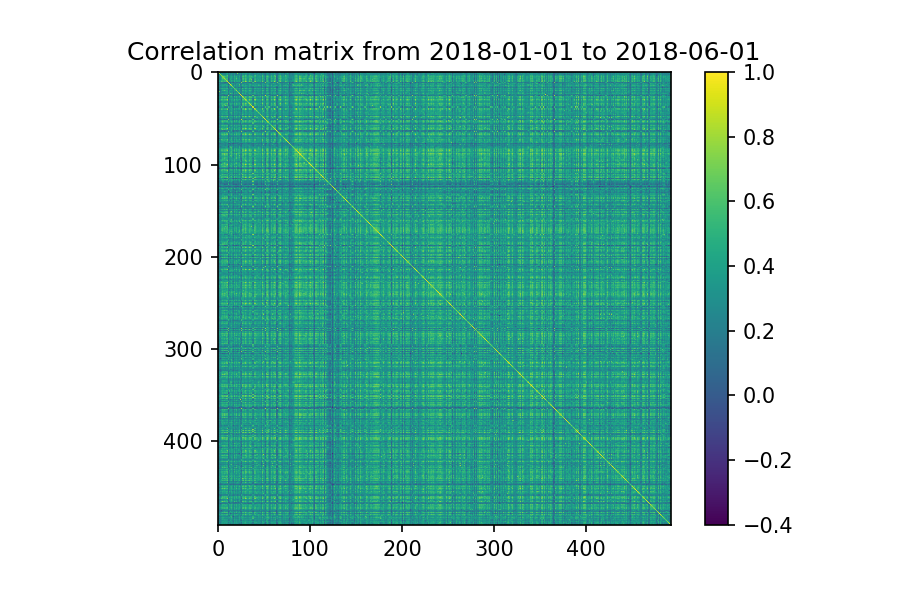
Ok, você seria louco de analisar essa matriz manualmente. Vamos partir para o motivo desse post que é usar nSBM.
Criando o grafo completo e filtrando
Como queremos explorar as comunidades usaremos apenas as correlações positivas,
pos_correlation = correlation_matrix.copy()
# vamos considerar apenas as correlações positivas pois queremos
# apenas as comunidades
pos_correlation[pos_correlation < 0.] = 0
# diagonal principal é setada a 0 para evitar auto-arestas
np.fill_diagonal(pos_correlation.values, 0)
Agora basta construir o grafo não direcionado associando os pesos das arestas com a correlação entre os ativos.
g = ig.Graph.Weighted_Adjacency(pos_correlation.values, mode='undirected')
# criamos uma feature symbol para cada vértice
g.vs["symbol"] = returns_all.columns
# o grafo pode estar desconectado. Portanto, extraímos a componente gigante
cl = g.clusters()
g = cl.giant()
n_edges_before = g.ecount()
Agora iremos aplicar o filtro de disparidade do edgeseraser para remover as arestas que não são significativas
_ = filter_ig_graph(g, .25, cond="both", field="weight")
cl = g.clusters()
g = cl.giant()
n_edges_after = g.ecount()
print(f"Percentage of edges removed: {(n_edges_before - n_edges_after)/n_edges_before*100:.2f}%")
print(f"Number of remained stocks: {len(symbols)}")
Percentage of edges removed: 95.76%
Number of remained stocks: 492
A maior parte das arestas foi removida. Será que conseguimos fazer algo com esse grafo compactado?
nSBM: buscando hierarquia e comunidades
Convertendo o iGraph em graph-tool
O graph-tool é um pacote com excelente desempenho, mas para ganhar essa performance ele exige um pouquinho mais de trabalho tais como declarar o tipo dos dados. O primeiro passo para usar o graph-tool é converter nosso grafo iGraph para uma instância dele
import graph_tool.all as gt
gnsbm = gt.Graph(directed=False)
# iremos adicionar os vértices
for v in g.vs:
gnsbm.add_vertex()
# e as arestas
for e in g.es:
gnsbm.add_edge(e.source, e.target)
Inferência dos blocos
Com o grafo construído iremos executar o algoritmo de inferência de blocos. Esse algoritmo executa uma minimização do que é conhecido como “description length” do modelo Bayesiano. Em um post futuro falarei um pouco sobre a matemática se você se já estiver interessado dê uma olhada no artigo original do Tiago Peixoto aqui.
state = gt.minimize_nested_blockmodel_dl(gnsbm)
O código abaixo é só para gerar as cores para nosso plot
symbols = g.vs["symbol"]
sectors = [symbol2sector[symbol] for symbol in symbols]
u_sectors = np.sort(np.unique(sectors))
u_colors = [plt.cm.tab10(i/len(u_sectors))
for i in range(len(u_sectors))]
# a primeira cor da lista era muito similar a segunda,
u_colors[0] = [0, 1, 0, 1]
sector2color = {sector: color for sector, color in zip(u_sectors, u_colors)}
rgba = gnsbm.new_vertex_property("vector<double>")
gnsbm.vertex_properties['rgba'] = rgba
for i, symbol in enumerate(symbols):
c = sector2color[symbol2sector[symbol]]
rgba[i] = [c[0], c[1], c[2], .5]
Executaremos o método draw para gerar o plot. O parâmetro que talvez você queira brincar um pouco é o $\beta \in (0, 1)$. Tal parâmetro é responsável pela força do edge-bundling, ou seja, a força com que as arestas serão atraídas uma à outra. Este parâmetro tem finalidades apenas para facilitar a visualização, não existe nenhuma relação com o nSBM.
options = {
'output': f'nsbm_{start_date}_{end_date}.png',
'beta': .9,
'bg_color': 'w',
#'output_size': (1500, 1500),
'vertex_color': gnsbm.vertex_properties['rgba'],
'vertex_fill_color': gnsbm.vertex_properties['rgba'],
'hedge_pen_width': 2,
'hvertex_fill_color': np.array([0., 0., 0., .5]),
'hedge_color': np.array([0., 0., 0., .5]),
'hedge_marker_size': 20,
'hvertex_size':20
}
state.draw(**options)
Finalmente, agora é só ver o resultado da nossa filtragem e inferência
plt.figure(dpi=150)
plt.title(f"Sectors of the S&P 500 from {start_date} to {end_date}")
legend = plt.legend(
[plt.Line2D([0], [0], color=c, lw=10)
for c in list(sector2color.values())],
list(sector2color.keys()),
bbox_to_anchor=(1.05, 1),
loc=2,
borderaxespad=0.)
plt.imshow(plt.imread(f'nsbm_{start_date}_{end_date}.png'))
plt.xticks([])
plt.yticks([])
plt.axis('off')
plt.savefig(f'nsbm_final_{start_date}_{end_date}.png', bbox_inches='tight',
dpi=150, bbox_extra_artists=(legend,), facecolor='w', edgecolor='w')
plt.show()

Ok, muito bonito! Conseguimos ver agrupamentos de certos setores, algumas misturas, muitas conexões entre o Financials e Industrials, etc. Se você não consegue ver isso agora vou tentar te explicar como interpretar esse gráfico.
Como analisar?
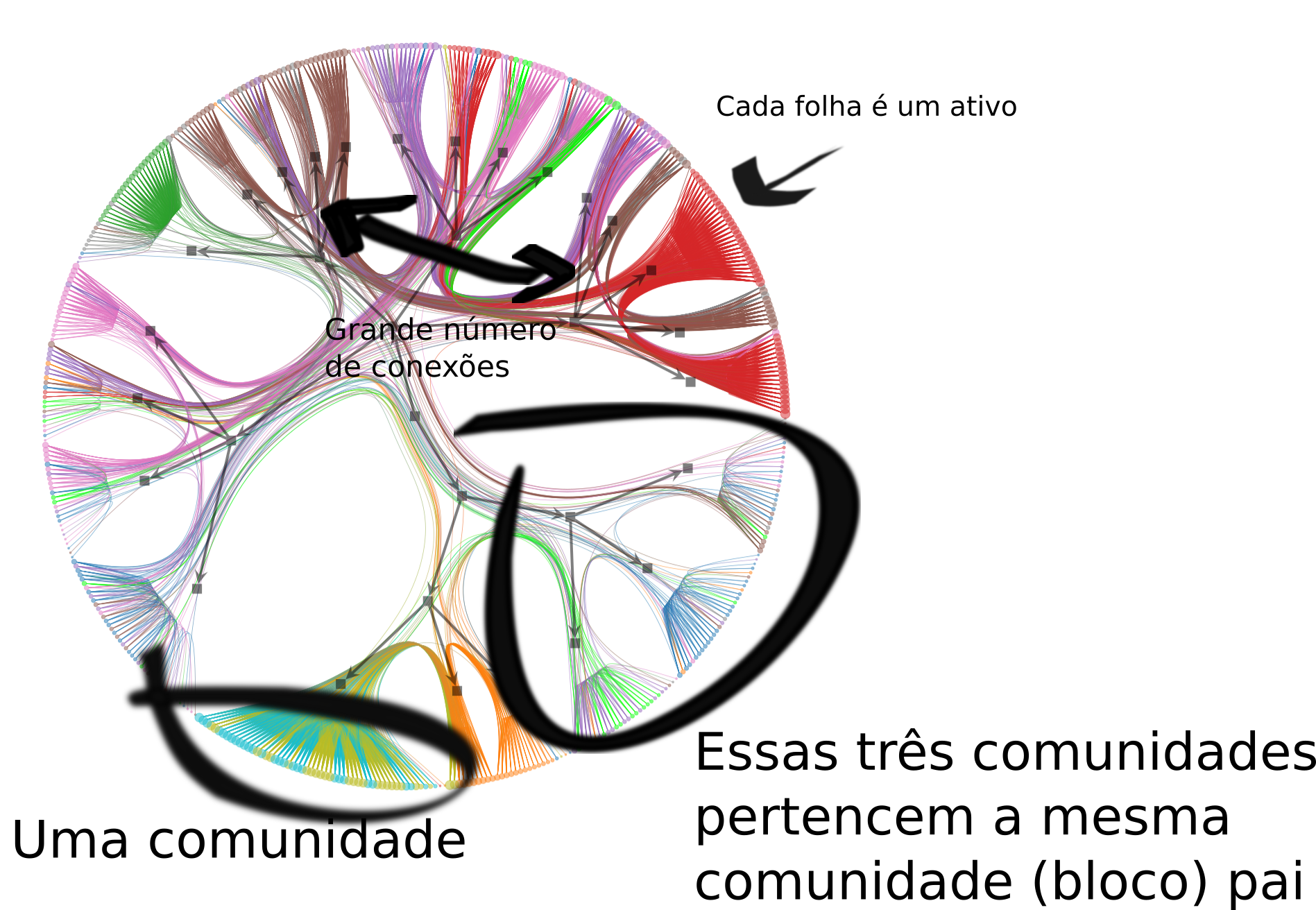
- Cada círculo no conjunto que parece a escova de uma vassoura é um ativo, um vértice do grafo original.
- Cada escova é uma comunidade de ativos. Podemos navegar na hierarquia seguindo o caminho reverso apontado pelas setinhas no grafo em preto. Veja que na imagem eu coloquei como exemplo três comunidades que pertencem à mesma comunidade pai. Uma coisa interessante que podemos observar é que a maior parte dos ativos relacionados a Consumer staples forma uma comunidade com Real state e Utilities no segundo nível.
E as arestas?
- Podemos notar que um grande número de conexões entre Financials, Industrials e Information technology sobreviveram ao filtro de disparidade. Sendo um indicativo que esses ativos têm uma forte relação nos retornos. Ok, antes eu falei que o $\beta$ controla o efeito de atração entre as arestas, veja o que acontece se eu reduzir o $\beta$ para $0.5$:

Você também pode explorar o resultado do nSBM manualmente. Para obter um sumário da hierarquia das comunidades obtidas pelo nSBM podemos invocar o método print_summary
state.print_summary()
l: 0, N: 483, B: 25
l: 1, N: 25, B: 6
l: 2, N: 6, B: 2
l: 3, N: 2, B: 1
l: 4, N: 1, B: 1
No nível de folhas temos os ativos. No primeiro nível temos 21 comunidades para os 11 setores.
Supondo que você queira obter quais comunidades um dado ativo pertence, no caso “TSLA”,
# esse é o indice da TSLA no nosso grafo original
symbol = "TSLA"
index_tesla = symbols.index(symbol)
symbol, symbol2sector[symbol], symbol2name[symbol]
('TSLA', 'Consumer Discretionary', 'Tesla')
Para obter as comunidades que o TSLA pertence percorremos a hierarquia de baixo para cima, até a raiz
# para obter os indices
r0 = state.levels[0].get_blocks()[index_tesla]
r1 = state.levels[1].get_blocks()[r0]
r2 = state.levels[2].get_blocks()[r1]
r3 = state.levels[3].get_blocks()[r2]
(r1, r2, r3)
(19, 0, 0)
Você pode explorar as comunidades usando essa abordagem. Contudo, eu recomendo você usar o THREE.js ou D3 para realizar essa exploração. Futuramente disponibilizarei meu código para permitir uma visualização interativa do nsbm usando threejs direto no browser!
Outras aplicações de nSBM
nSBM’s e SBM’s encontram diversas aplicações como NLP e em um trabalho recente meu em análise de surveys.
Extras: MST
Eu prometi mostrar como ficaria o mesmo universo de dados usando MST (árvores de expansão mínima). A intuição por trás do MST é que queremos construir um grafo esparso de um grafo original, tal que as somas dos pesos das arestas seja a menor possível sem desconectar os vértices do grafo. Veja mais aprofundado aqui.
Convertendo correlações em distâncias
A primeira coisa que precisamos fazer é converter a matriz de correlação em uma matriz de distância. Isso pode ser feito usando a seguinte função
$d(\mathrm{stock}_1, \mathrm{stock}_2) = \sqrt{2(1-\mathrm{corr}(\mathrm{stock_1}, \mathrm{stock}_2))}$
dist_matrix = np.sqrt(2*(1-correlation_matrix))
dist_matrix = dist_matrix.fillna(0)
np.fill_diagonal(dist_matrix.values, 0)
Extraindo o MST
O igraph já implementa um algoritmo para extrair o MST de um grafo de forma eficiente, mesmo que o grafo seja completo. Nossa matriz de correlação é um grafo completo!
g = ig.Graph.Weighted_Adjacency(dist_matrix.values, mode='undirected')
g = g.spanning_tree(weights="weight", return_tree=True)
g.vs["symbol"] = returns_all.columns
sectors = [symbol2sector[symbol] for symbol in returns_all.columns]
colors = [
sector2color[sector] for sector in sectors
]
Visualizando o MST
Agora com nosso MST vamos usar um layout de grafos bem simples para visualizar nosso grafo
g.vs["color"] = colors
pos = g.layout_fruchterman_reingold(niter=10000, weights="weight")
pos = np.array(pos.coords)
Finalmente, nosso resultado:
from matplotlib.collections import LineCollection
lines = []
colors = []
for s, t in g.get_edgelist():
x0, y0 = pos[s]
x1, y1 = pos[t]
lines.append([(x0, y0), (x1, y1)])
colors.append("black")
lc = LineCollection(lines, colors=colors, zorder=0, alpha=.5)
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1)
ax.scatter(
pos[:, 0],
pos[:, 1],
c=g.vs["color"],
s=25,
marker="d",
alpha=.8,
zorder=1
)
ax.add_collection(lc)
ax.axis('off')
legend = ax.legend(
[plt.Line2D([0], [0], color=c, lw=10)
for c in list(sector2color.values())],
list(sector2color.keys()),
bbox_to_anchor=(1.05, 1),
loc=2,
borderaxespad=0.)
plt.savefig(f'mst_{start_date}_{end_date}.png', bbox_inches='tight',)
plt.show()
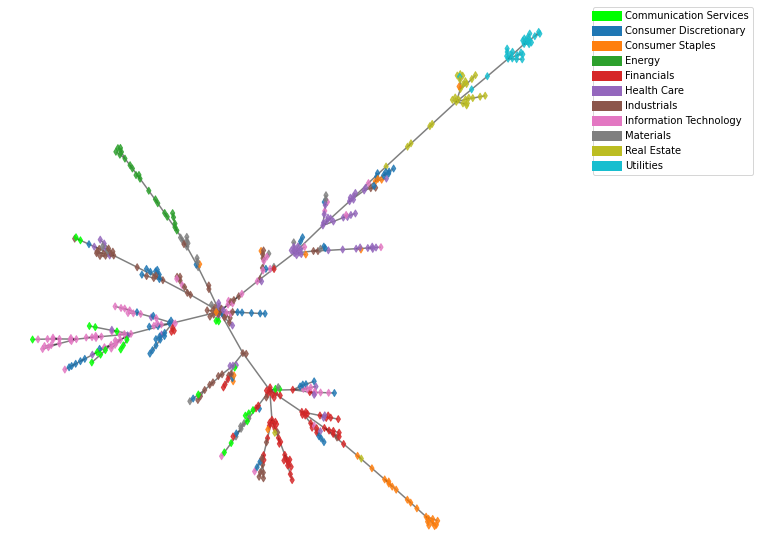
Alguns padrões aparecem, mas o MST é muito menos rico de informações que o nSBM, exploraremos mais essas vantagens em posts futuros.
Agradecimentos
Agradeço ao Maike Reis e Felipe Santos pelas dicas e correções.