Correlação entre Ativos no Python

Correlação entre Ativos no Python published at the "Open Code Community"

Calculando a variância e a volatilidade de uma carteira hipotética

Neste post, vamos mostrar como analisar a correlação entre ativos usando Python. Também montaremos uma carteira hipotética, indicando como utilizar a matriz de correlação para calcular a volatilidade da carteira. Iremos comparar esse método com a forma de obter a informação direto a partir das rentabilidades de cada holding.

Primeiro, o que é covariância? É uma medida do grau de interdependência entre duas variávies aleatórias. No nosso caso, estamos considerando que os preços de fechamento dos ativos são variáveis aleatórias. A relação da correlação ou, mais especificamente, coeficiente de correlação de Pearson com a covariância é a seguinte:

\begin{align} \rho_{XY} = corr (X, Y) = \dfrac{cov(X,Y)}{\sigma_X \cdot \sigma_Y }\end{align}

Legenda:

• $corr(X,Y) = \rho_{XY}$ é o coeficiente de correlação de Pearson

• $cov(X,Y)$ é a covariância entre $X$ e $Y$

• $\sigma_X$ e $\sigma_Y$ são os desvios padrões de $X$ e $Y$

Então, o coeficiente de correlação de Pearson é a normalização da covariância, variando entre $-1$ e $1$.

Quando o coeficiente entre duas variáveis $X$ e $Y$ está mais perto de $1$, significa que há uma correlação positiva. Então, por exemplo, se $X$ aumenta, é provável que $Y$ também aumente. Simultaneamente, se $X$ diminui é provável que $Y$ também diminui. Se o coeficiente está mais perto de $-1$, as variávies são correlacionáveis negativamente. A ideia é: se uma sobe, a outra dimui e vice-versa. Por fim, se o coeficiente é $0$, não existe uma dependência linear. Isso não exlui outras dependências ou relações.

Vale ressaltar que correlação não implica casualidade. Também, falando matematicamente, correlação não é transitiva, ou seja, se $A$ é positivamente correlacionado com $B$ e $B$ é positivamente correlacionado com $C$, não implica que $A$ é positivamente correlacionado com $C$.

Importando as bibliotecas

import yfinance as yf
import pandas as pd 
import numpy as np
import statsmodels.api as sm #### biblioteca para plotar correlacao
import matplotlib.pyplot as plt

Extraindo os dados

Vamos utilizar a biblioteca yfinance para exportar os preços de fechamento de ativos. Para os ativos, escolhi ETFs americanos setoriais, de modo a exemplificar a correlação entre setores da economia.

etf_lista = ['SPY', 'GLD', 'XLE', 'XLF', 'XLI', 'XLP']
## extrair dados de uma vez com yf.download
etf = ' '.join(etf_lista)
df  = yf.download (etf, 
                   period = "2y",
                   interval = "1d",
                   group_by = 'ticker', ## poderá chamar df[ticker]
                   progress = False)

Veja as informações que o yfinance importa para cada holding: preço de abaertura, preço mais alto, preço mais baixo, preço de fechamento, preço de fechamento ajustado e volume.

df['SPY'].columns

Vamos calcular o retorno diário para cada ativo:

### Calcular rentabilidade usando pct_change
for etf in etf_lista:
df[(etf, 'Return')] = df[(etf, 'Close')].pct_change()  

Agora, vamos criar um dataframe apenas com a rentabilidade de cada ETF.

### dataframe dg apenas com rentabilidades de cada etf 
colunas = list()
for elem in etf_lista:
    colunas.append((elem, 'Return'))
dg = df.filter(items=colunas)
dg.columns = etf_lista ### muda nome das colunas
dg.head()

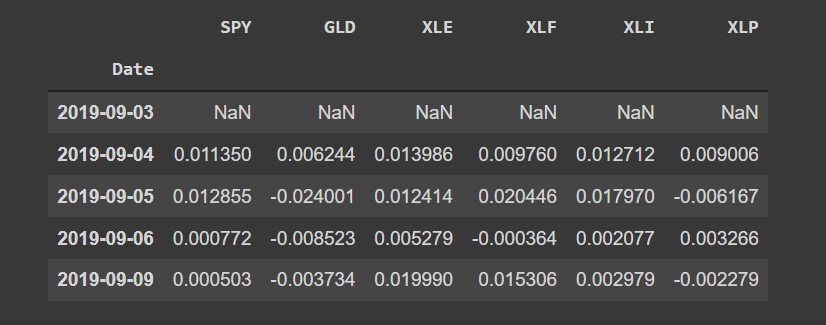
Finalmente, após obtermos o dataframe da rentabilidade, podemos calcular a matriz correlação entre os ativos. A biblioteca pandas tem uma função para isso - corr() - e a biblioteca statsmodels.api tem uma função que vai fazer uma mapa de calor para a matriz de correlação. O resultado fica bem interessante.

correlacao = dg.corr()
#plotar correlação
sm.graphics.plot_corr(correlacao, xnames=correlacao.columns)
plt.title("Matriz de Correlação")
plt.show()

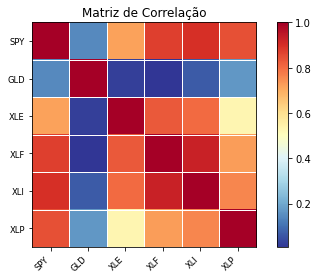
correlacao

##Calculando a variância e a volatilidade de uma carteira hipotética

Primeiro, vamos definir o portfólio.

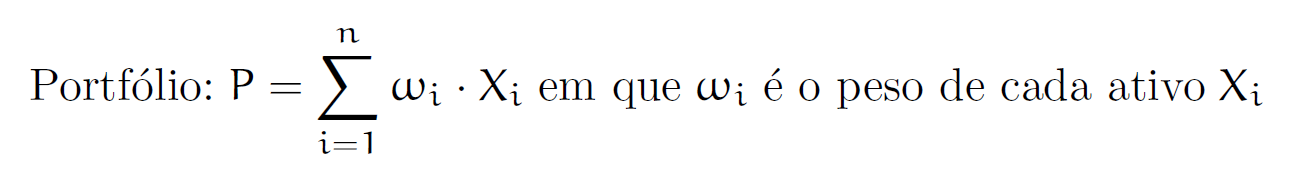
A partir da definição de variância e correlação, podemos obter:

\begin{align} Var(P) = Var( \sum_{i=1}^{n} \omega_i \cdot X_i) = \sum_{1 \leq i, j \leq n}^{} \omega_i \cdot \omega_j \cdot cov(X_i, X_j) \end{align}

\begin{align} Var(P) = \sum_{1 \leq i, j \leq n}^{} \omega_i \cdot \omega_j \cdot \rho_{X_iX_j} \cdot \sigma_i \cdot \sigma_j \end{align} \begin{align} Var(P) = \sum_{j=1}^{n} \sum_{i=1}^{n} (\omega_i \cdot \sigma_i) \cdot(\omega_j \cdot \sigma_j )\cdot \rho_{X_iX_j} \end{align}

Contudo, a soma dupla pode ser vista como uma multiplicação de matrizes.

Então, a variância do portfólio pode ser calculada pela multiplicação da matriz do peso de cada holding pela seu respectivo desvio padrão (ou volatilidade) e da matriz de correlação (a famosa matriz desse post - no caso a do meio). Vamos para o código!

### calcular desvio padrão do portfólio de etf usando matriz de correlação
pesos = [30, 10, 15, 25, 10, 20]
dvp = dg.std() ### serie de desvio padrão para cada etf
matriz = pesos*dvp
### para multiplicar de matrizes, pode utilizar np.matmul ou np.dot
# port_var = np.matmul(matriz, np.matmul(correlacao, matriz))
port_var = np.dot(matriz, np.dot(correlacao, matriz))

Assim, calculamos a variância da carteira. Para calcular o desvio padrão do portfólio e, portanto, a volatilidade, basta calcular a raiz quadrada da variância.

port_dvp = np.sqrt(port_var)
port_dvp

Alternativamente, poderíamos ter calculado a volatilidade da carteira de outra forma. Considere o produto de matriz entre as rentabilidades de cada ativo e o peso de cada ativo na carteira. Assim, teremos o quanto nossa carteira rendeu por dia. Podemos usar a função std para calcular o desvio padrão da nossa carteira.

carteira = np.dot(dg, pesos)
carteira = pd.DataFrame(carteira)
carteira_dvp = carteira.std()
carteira_dvp[0]

Será que os dois valores calculados são iguais?

carteira_dvp[0] - port_dvp

A ordem do erro está em $10^{-15}$, ou seja, dentro da expectativa dos erros de aproximações.

Ambos os métodos são rápidos. Porém, o primeiro também permite visualizar a correlação entre os ativos, o que permite uma análise de se e quanto você está exposto ao risco.